Matematické Fórum

Ahoj,
nechť má pravidelný šestiúhelník S stranu délky n a nechť útvar U vznikne spojením dvou rovnostranných trojúhelníků o straně 1, které k sobě přiložíme svými stanami (tj. U je kosočtverec). Nechť pomocí kopií 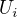útvaru U vyplníme celý S tak, že kratší úhlopříčka každé 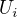je rovnoběžná s některou stranou S (tj. vrcholy 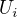i vrcholy S leží ve vrcholech trojúhelníkové sítě tvořené rovnostrannými trojúhelníky o straně délky 1). Potom lze tedy množinu všech 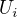rozdělit na tři množiny (A,B,C), podle toho se kterou stranou S je kratší úhlopříčka 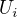rovnoběžná (S má vždy dvě strany rovnoběžné, tedy množiny jsou opravdu tři a nikoli šest). Dokažte, že potom je |A|=|B|=|C|.