Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Fyzika
- » dá sa vybrať náboj z integralu pri intenzite elektrostatického poľa?
#1 19. 02. 2015 16:37
- miso16211
- Πυθαγόραc
- Příspěvky: 1522
- Pozice: n/a
dá sa vybrať náboj z integralu pri intenzite elektrostatického poľa?
zdravím, riešim dilemu, na základnom kurze elektromagnetizmus sme mali intezitu elektrostatického poľa pre diskrétne a spojité rozloženie nábojov.
Pre diskrétne rozloženie n nábojov platí 
Pre spojité rozloženie platí 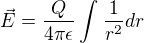
Otázka: Prečo sme pri spojitom rozložení mohli vybrať Q? Q je celkový náboj v nejakom trebárs telese? Ja si myslím, že náboj by mal byť vo vnútri integrálú ako dQ.
Teda podľa mňa, by to malo byť takto : 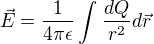 Ktoré vyjadrenie pre spojité rozloženie nábojov je správne? Ďakujem.
Ktoré vyjadrenie pre spojité rozloženie nábojov je správne? Ďakujem.
Offline
#2 19. 02. 2015 22:25 — Editoval pietro (19. 02. 2015 22:26)
Re: dá sa vybrať náboj z integralu pri intenzite elektrostatického poľa?
↑ miso16211: Ahoj, druhý a tretí vzťah sa mi zdajú podozrivé ...
zle si možno niečo odpísal...
Postup : radšej si prelúskaj intenzitu v kľude a zafixuj z tohoto
http://cs.wikipedia.org/wiki/Intenzita_ … %A9ho_pole
uvedom si, že či používaš jednotkový vektor (==> 1/r^2) alebo plohový vektor od náboja Q (==>1/r^3)
Potom prerátaj jednotlivé príklady na diskrétne bodové náboje
tu... http://fyzikalniulohy.cz/uloha.php?uloha=18 ( a použi vzorec z WIKI)
dostaneš zručnosť v predstave ako funguje intenzita od vektora polohy.
A potom prejdeš na spojité zmeny náboja v priestore.
Z integrálu zásadne vyberáme len konštanty, ktoré vôbec nezávisia na premennej podľa ktorej integrujeme ..dx
Offline
#3 20. 02. 2015 13:42 — Editoval miso16211 (20. 02. 2015 14:01)
#4 21. 02. 2015 10:17
Re: dá sa vybrať náboj z integralu pri intenzite elektrostatického poľa?
↑ miso16211:Ahoj, tu http://www.elsoc.net/coursenotes/ELEC31 … pter2a.pdf
na str.4/9 je nezarámovaný , zrejme preto, lebo pre praktické účely sa užívajú iné vzťahy, pozri nasled. strany.
Treba si uvedomiť poriadne význam všetkých veličín vo vzťahu a to je najlepšie na príkladoch.
=====
Aj tu http://www.cems.uvm.edu/~keoughst/Lectu … und%29.pdf
na str. 14/28.
==============
Na fyziku prof. Krempaského sa možno vždy len spoľahnúť !
Offline
#5 22. 02. 2015 14:15
#6 22. 02. 2015 16:16 — Editoval pietro (22. 02. 2015 16:24)
Re: dá sa vybrať náboj z integralu pri intenzite elektrostatického poľa?
↑ miso16211: Všetky vzťahy, ktoré vychádzajú zo základnej definície
E=F/q ( vektorovo) a súčasne v nich neurobíme myšlienkovú chybu,
sú správne.
==============
A keďže nemáme čas ani prostriedky na overovanie experimentom, dobré je riešiť príklady. Tam si postupy ozrejmíme najlepšie.
Offline
#7 22. 02. 2015 16:30
Re: dá sa vybrať náboj z integralu pri intenzite elektrostatického poľa?
↑ miso16211:
No tak to vezmeme postupně.
1. Předpokládám, že mám spojitě rozložený náboj. Toto rozložení nám udává veličina nazývaná hustota náboje.
Označme jí 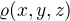 Doufám, že její definici a vůbec co to je víš.
Doufám, že její definici a vůbec co to je víš.
2. Hledejme velikost intenzity v bodě 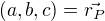
(teď to bude již řečeno spíš fyzikálně než matematicky ale snad to bude srozumitelné)
3. Teď uvažujeme malý objemový element dV nacházející se v prostoru v bodě se souřadnicemi (x,y,z).
4. Vzdálenost od bodu, ve kterém budeme hledat intenzitu je 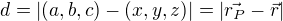 kde r je polohový vektor elementu dV
kde r je polohový vektor elementu dV
5. Vektor, který má velikost 1 a směřuje od elementu dV k bodu (a,b,c) je zřejmě 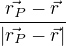
6. Pak zřejmě platíí 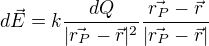 kde k značí konstantu z coulumbova zákona, ten první zlomek i udává velikost (úměrná náboji, nepřímo úměrná čtverci vzdálenosti) poslední zlomek mi udává směr, a navíc nemění velikost
kde k značí konstantu z coulumbova zákona, ten první zlomek i udává velikost (úměrná náboji, nepřímo úměrná čtverci vzdálenosti) poslední zlomek mi udává směr, a navíc nemění velikost
7. 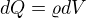
8. Pak přirozeně 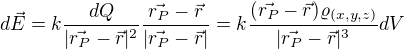
9. Celkovou intenzitu pak určíme integrací přes celý prostor, jelikož jediné co tam nezáleží na (x,y,z) je k, tak jediné co můžu vytknout před integrál je k.
Offline
#9 23. 02. 2015 16:46 — Editoval miso16211 (23. 02. 2015 16:46)
- miso16211
- Πυθαγόραc
- Příspěvky: 1522
- Pozice: n/a
Re: dá sa vybrať náboj z integralu pri intenzite elektrostatického poľa?
↑ Brzls: jedna otázka : nemožem namiesto rozdielu vektorov rp a r dat len jeden vektor r a to takého, ktorý ma počiatok v objemovom elementu a koniec v mieste v ktorom vyšetrujeme intenzitu?
PS.: 2 druháci ktorý tento predmet absolvovali uspesne mi jednoznačne tvrdili, že Q sa dá vyjmout pred integrál. Ani neviem či vôbec sa nejako dá napísať namiesto dQ náboj Q?
Ďakujem obom.
Offline
#10 23. 02. 2015 18:45 — Editoval Brzls (23. 02. 2015 18:55)
Re: dá sa vybrať náboj z integralu pri intenzite elektrostatického poľa?
↑ miso16211:
No tak jako děm dvoum druhákům bych doporučil aby si ten předmět zapsali ještě jednou...
Ledaže byste si nerozuměli a oni akorát mluvili o nějakém speciálním případě.
Samozřejmě ten rozdíl si můžeš označit nějakým jiným jediným písmenem, pokud ho vhodně definuješ,a hlavně pokud to pak v praxi správně použiješ!!
Je jasné že ti vůbec nic nebrání zavést značení co já vim např.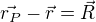
být tebou tak si přímo z definice zkusím vypočítat pár příkladů (které jdou klidně spočítat i jednodušším způsobem)
Například. Pole nabitého prstence (na ose)
Pole nabitého disku (opět pouze na jeho ose)
Pole nabité přímky
Pole nabité roviny
a klidně i polo nabité koule
Sám potom uvidíš jak se to počítá, co přesně co znamená a hlavně že nějakym kouzelnym způsobem vytíkání Q před integrál nefunguje
Taky by bylo dobrý aby si napsal, jak by vypadal ten tvůj vztah když vytkneš Q. Protože když se koukneš na svůj první příspěvek kde něco takového uvádíš, tka je jasné vidět že to je blbost, protože to co by ti z toho vylezlo by mělo rozměr potenciálu, nikoli intenzity
Offline
#11 24. 02. 2015 09:21
Re: dá sa vybrať náboj z integralu pri intenzite elektrostatického poľa?
↑ miso16211: a ešte takouto ilustráciou sa to dá priblížiť.
Offline
Stránky: 1
- Hlavní strana
- » Fyzika
- » dá sa vybrať náboj z integralu pri intenzite elektrostatického poľa?
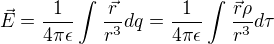
 je objemová hustota náboja
je objemová hustota náboja
