Matematické Fórum

seized · 17. 02. 2015 21:18

Zdravim, potreboval by som pomoct s takouto limitou:
$\lim_{x\to-1}\frac{\sqrt{\pi }-\sqrt{arccos x}}{\sqrt{x+1}}$

avsak nesmiem pouzit lopitalovo pravidlo, zaujima ma postup ako upravit tu limitu a dopracovat sa k vysledku bez pouzitia lopitalovho pravilda vysledok je $\frac{1}{\sqrt{2\pi }}$

Vopred dakujem za navrhy a napady

Pavel · 17. 02. 2015 21:30

↑ seized:

Obávám se, že limita tak, jak je zapsána, neexistuje.

Sergejevicz

EDIT: Opravena chyba, na kterou upozorňuje jeden kolega v dalším příspěvku.
EDIT 2: Odstranil jsem označení 1), protože 2), 3) atd. jsem v originále jaksi zapomněl použít.

Takže. Původně jsem na toto fórum chtěl psát něco k jinému tématu, ale zaujal mě tenhle příklad. Vyjde to, ale chce to nějakou tu práci.

Předně, ta limita musí být pro x jdoucí k -1 zprava, protože pro x < -1 není funkce definována.

A teď co s tím dělat.

Použijeme substituci y = arccos(x) a pro přejití k limitě pro y jdoucí k $\lim_{x\to -1+} \arccos(x) = \pi$ , a to zleva - viz chování arccos, budeme chtít použít větu o limitě složené funkce (VLSF). Jak je ovšem známo, k jejímu použití potřebujeme splnění alespoň jedné z jistých dvou podmínek.

Jedna z těch podmínek pro tento případ je, že arccos (coby vnitřní funkce) nenabývá hodnoty pí (coby své limity pro x jdoucí k -1 zprava) alespoň na nějakém (dokonce na žádném) pravém redukovaném okolí bodu -1, a to splněno je, protože arccos je funkce ryze monotónní.

Pak ještě existuje druhá podmínka, že totiž vnější funkce, což po aplikaci uvedené substituce je $\frac{\sqrt{\pi}-\sqrt{y}}{\sqrt{\cos(y)+1}}$ , je spojitá v pí, tato ale splněna není, neb není v pí díky jmenovateli definována.

Nicméně splnění první podmínky nám dovoluje přenést se použitím VLSF k limitě $\lim_{y\to\pi-}\frac{\sqrt{\pi}-\sqrt{y}}{\sqrt{\cos(y)+1}}$ .

Nyní si všimneme, že ve jmenovateli je pod odmocninou výraz, který by se vhodným rozšířením a úpravami dal upravit na známou limitu 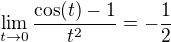$\lim_{t\to 0}\frac{\cos(t)-1}{t^2}=-\frac{1}{2}$ , ta se mimochodem počítá s využitím základní limity $\lim_{t\to 0}\frac{\sin(t)}{t}=1$ . Toto vhodné rozšíření je výrazem $\sqrt{(y-\pi)^2}$ . Po tomto rozšíření rozdělíme celý limitěný výraz na součin $\frac{\sqrt{\pi}-\sqrt{y}}{\sqrt{(y-\pi)^2}}\cdot\sqrt{\frac{(y-\pi)^2}{\cos(y)+1}}$ .

Použijeme větu o limitě součinu, jejíž použití bude odůvodněno smysluplností výsledku.

V prvním činiteli převedeme jmenovatele na absolutní hodnotu a uvážíme, že limitíme ypsilonem zleva, tím odstraníme i tuto absolutní hodnotu a pak už jen stačí rozšířit první činitel jeho čitatelem s plusem, něco se zkrátí a vzejde výraz $\frac{1}{\sqrt{\pi}+\sqrt{y}}$ , jehož limita pro y -> pi zleva je zřejmě reálné číslo.

Ve druhém činiteli je třeba nejprve aplikovat opět VLSF s druhou odmocninou coby vnější funkcí a celým argumentem této odmocniny coby funkcí vnitřní.

Limita vnitřní funkce je už skoro výše zmíněná známá limita, rozvedu případně v jiném příspěvku, každopádně to také vyjde reálné číslo (totiž 2) z definičního oboru (vnější) odmocniny a spojitost této odmocniny je odůvodněním pro výše zmíněné použití VLSF.

Součin dvou reálných čísel je reálné číslo (a je to také ten celkový výsledek), čímž je odůvodněné použití věty o limitě součinu.

Hele, jednodušší by pro mě bylo nahrát sem pár papírů, jak jsem to dělal, než to tady popisovat, stojí mě to daleko víc času, jenže to by mě pak zas někdo udělil mínusový bod za přílišné razení, že? Ale klidně pište, jak naložit s těmi věcmi, které jsem tu nerozváděl. Dávám pravda celkem důraz na odůvodňování a korektnost kroků, inu k tomu nás na škole vychovali.

Pavel · 21. 02. 2015 00:36

↑ Sergejevicz:

Správně by mělo být

$\lim_{t\to 0}\frac{\cos(t)-1}{t^2}={\color{red}-}\frac{1}{2}$

Freedy · 21. 02. 2015 00:42

↑ Sergejevicz: kolikátým rokem jsi na matfyzu?

Sergejevicz

↑ Pavel:
Máš pravdu, omlouvám se za chybu, opravil jsem to.

Sergejevicz · 21. 02. 2015 09:49

↑ Freedy:
Já už tam nejsem, asi před rokem jsem absolvoval magistra.

seized · 26. 02. 2015 18:11 — Editoval seized (26. 02. 2015 18:12)

Dakujem pekne, uz sme nato prisli v skole so spoluziakom a presne tento postup bol ucinny ( kludne nahraj par papierov mna zaujima postup a nie vysledok ;) ) a kebyze nasiel som este takuto limitu a tiez je celkom zaujimava a mam problem na nu prist
$\lim_{x\to0}\frac{1-\cos (1-\cos x)}{x^4}$

vysledok ma byt [ $\frac{1}{8}$ ]

holyduke · 26. 02. 2015 18:59

↑ seized: čau, třeba takhle:
použiješ L´H a máš
$\lim_{x\to0}\frac{\sin (1-\cos x)\cdot \sin x}{4x^3}=\lim_{x\to0} \frac{\sin x}{x}\frac{\sin (1-\cos x)}{4x^2}$
první výraz se z zřejmě rovná 1 a na druhý opět L´H
$=\lim_{x\to0} \frac{\cos (1-\cos x)\sin x}{8x}=\lim_{x\to0} \frac{\sin x}{x}\cdot \frac{\cos (1-\cos x)}{8}=\frac{1}{8}$

Sergejevicz · 26. 02. 2015 19:11

↑ holyduke:
Jenže tady nejspíš jde o to, jak to udělat bez L'H, podobně jako v předchozím případě. Viz totok :-).

holyduke · 26. 02. 2015 19:16

↑ Sergejevicz:
toho jsem si bohužel nevšiml, děkuji za doplnění

Matematické Fórum

#1 17. 02. 2015 21:18

limita

#2 17. 02. 2015 21:30

Re: limita

#3 20. 02. 2015 22:33 — Editoval Sergejevicz (26. 02. 2015 20:02)

Re: limita

#4 21. 02. 2015 00:36

Re: limita

#5 21. 02. 2015 00:42

Re: limita

#6 21. 02. 2015 09:48 — Editoval Sergejevicz (21. 02. 2015 13:08)

Re: limita

#7 21. 02. 2015 09:49

Re: limita

#8 26. 02. 2015 18:11 — Editoval seized (26. 02. 2015 18:12)

Re: limita

#9 26. 02. 2015 18:59

Re: limita

#10 26. 02. 2015 19:11

Re: limita

#11 26. 02. 2015 19:16

Re: limita

Zápatí