Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » dokaz - kombinatorika (TOTO TÉMA JE VYŘEŠENÉ)
#1 01. 03. 2015 16:12 — Editoval jelena (01. 03. 2015 17:33)
- geovektor1
- Příspěvky: 119
- Reputace: 0
dokaz - kombinatorika
Ahoj, narazil som na zaujimavu ulohu, mam dokazat vlastnosti ale neviem ako na to, znenie:
Dokazte nasledujuce rovnosti  pre parne
pre parne 
a pre neparne
pre neparne  .
.
v oboch vyrazoch je ta minus jednicka umocnena na  a
a  ale neviem preco mi to tak blbo ukazalo /Jelena: opraveno.
ale neviem preco mi to tak blbo ukazalo /Jelena: opraveno.
Offline
- (téma jako vyřešené označil(a) geovektor1)
#3 01. 03. 2015 23:54
- geovektor1
- Příspěvky: 119
- Reputace: 0
Re: dokaz - kombinatorika
ja tomu taktiez uplne nerozumiem, preto som vas poprosil o pomoc, snad su tu matematici, ktori maju skusenost s kombinatorikou, original s knizky je takyto: http://www.fastimages.eu/images/123ffsdfsf.png
Offline
#4 02. 03. 2015 01:01
Re: dokaz - kombinatorika
Řekl bych, že půjde o použití multinomické věty (což je zobecnění binomické věty), která říká, že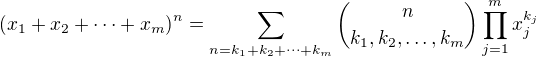
kde sčítáme přes všechny možné součty nezáporných celých čísel.
Takže např. pro sudé 

Pro liché  to bude obdobné
to bude obdobné
A je to! :-)
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » dokaz - kombinatorika (TOTO TÉMA JE VYŘEŠENÉ)

 ? A
? A 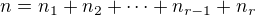 ? A proč v exponentu chybí
? A proč v exponentu chybí  ?
?