Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#7 06. 03. 2015 18:42
Re: logaritmické rovnice
↑ Takjo:
omlouvám se, špatně sem to opsal z papíru; mezikrokem by mělo být 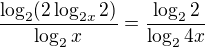
jak se to teda řeší dále (po "a zjednodušíme")? (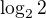 si převedu na 1; ale pak nevim co s tím podílem)… jestli by jste to mohl trochu rozepsat či popsat jak na to…Děkuji
si převedu na 1; ale pak nevim co s tím podílem)… jestli by jste to mohl trochu rozepsat či popsat jak na to…Děkuji
Offline

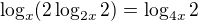
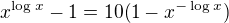
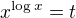
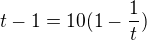
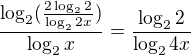 a zjednodušíme ...
a zjednodušíme ...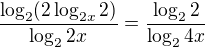 ?
?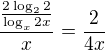 ? nebo takhle nejde odlogaritmovat podíl?
? nebo takhle nejde odlogaritmovat podíl?