Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#5 09. 03. 2015 15:44
Re: Lineární algebra - detekce podprostoru
↑ maver:
Třeba: implikace  neplatí, je-li
neplatí, je-li 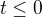 , takže
, takže  není podprostorem v
není podprostorem v 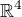 .
.
(U podprostoru by taková implikace musela platit pro libovolné reálné  - vedle daších vlastností, jimiž je
- vedle daších vlastností, jimiž je
podprostor jako pojem definován).
Offline
#6 09. 03. 2015 22:12 — Editoval maver (09. 03. 2015 22:37)
Re: Lineární algebra - detekce podprostoru
opět se omlouvám, ale nevím, jak pracovat s těmi nerovnostmi.
-------------------------------------
rozumím třeba tomuto: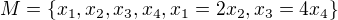
pak součet je: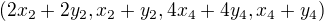
Vyšly mi tyto hodnoty a vidím, že jde o 
------------------------------------
ale nevím, jak mám napsat nerovnosti do podobného řádku a jak je možné, že mi má vyjít u původního příkladu tohoto diskusního vlákna s nerovnostmi (0,0,0,0) neleží v M
Offline
#7 09. 03. 2015 22:55
Re: Lineární algebra - detekce podprostoru
↑ maver:
Ahoj,
řekl bych, že se na vektorové prostory díváš způsobem "mechanicky to nějak spočítám" a uniká ti do podstatné. Zapomeň na chvíli na to, že máš nějaké naučené postupy a zamysli se jen nad definicí toho, co je vektorový prostor. Klidně si představuj "šipky z počátku" v R3, to pro začátek stačí. Nějaká podmnožina M v R3 bude vektorovým podprostorem vektorového prostoru R3, když si budeš moci vzít libovolný vektor z M, tak jeho libovolné protažení vč. smrsknutí na nulu a otočení (násobení záporným číslem) bude patřit do M. Jinými slovy, když bude v M vektor u, budou v M všechny vektory ležící na přímce určené vektorem u procházející počátkem. Podobně pro každé dva vektory z M bude v M i jejich součet. Tedy spolu s předchozím plyne, že když jsou v M vektory u a v, tak musí být v M u+v a vlastně celá rovina určená vektory u a v.
Když si to takhle představíš, mělo by ti být jasné, že takové množiny určené nerovností nejlépe otestuješ, tak, že si geometricky představíš, že každá přímka procházející počátkem buď celá leží v M nebo celá (s výjimkou počátku) neleží v M. Samozřejmě že do M, aby byla vektorový podporostor, musí patřit počátek, takže nejlepší je nejdřív si ověřit, zda počátek do M vůbec patří.
Takže se žádným "součtem nerovností" nemanipuluj, k řešení vede jiná cesta.
Доктор сказал «в морг» — значит в морг!
Offline
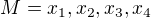


 je podprostor v
je podprostor v 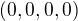 .
.