Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Odvození rovnice klotoidy (TOTO TÉMA JE VYŘEŠENÉ)
#1 03. 03. 2015 15:33 — Editoval FliegenderZirkus (03. 03. 2015 15:39)
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Odvození rovnice klotoidy
Ahoj,
chtěl bych si odvodit rovnice klotoidy, tedy rovinné křivky, jejíž křivost je přímo úměrná délce oblouku od zvoleného počátku.
Řekněme, že kartézské souřadnie jsou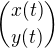 .
.
Dosadil jsem vzorečku na Wikipedii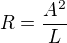
za poloměr křivosti
a za délku oblouku  ,
,
dohromady tedy .
.
Teď bude nejspíš potřeba argumentovat parametrizací pomocí délky oblouku, čímž se rovnice zjednodušší. Poradíte prosím jak to udělat „rigorózně“? :) Díky
Offline
- (téma jako vyřešené označil(a) FliegenderZirkus)
#2 04. 03. 2015 22:59
- Sergejevicz


- Příspěvky: 581
- Škola: Mgr. mat. a fyz. modelování na MFF UK v r. 2014
- Pozice: výpočtář
- Reputace: 21
- Web
Re: Odvození rovnice klotoidy
Vím, že klotoidu (Cornuovu spirálu) parametrizují tzv. Fresnelovy (čti "Frenelovy") integrály.
Něco je třeba tady:
http://www.google.cz/url?sa=t&rct=j … mp;cad=rja
http://en.wikipedia.org/wiki/Fresnel_integral
Kopáček: Mat. anal. nejen pro fyziky, Veselý: Zákl. mat. anal., Bečvář: Lin. alg., Matfyzpress
Bican: Lin. alg. a geom., Academia
Offline
#3 05. 03. 2015 13:22 — Editoval Brano (05. 03. 2015 14:16)
Re: Odvození rovnice klotoidy
ja by som na to isiel takto:
najprv si mozme uvedomit, ze krivku mozeme vzdy parametrizovat jej dlzkou -  (pocitanou od nejakeho bodu)
(pocitanou od nejakeho bodu)
potom sa nam zjednodusi aj polomer krivosti a prava strana je
a prava strana je  teda mame rovnicu
teda mame rovnicu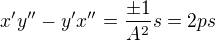 kde
kde  je nejaka nova konstanta no a este to, ze
je nejaka nova konstanta no a este to, ze  je dlzka znamena
je dlzka znamena
oznacme si  a
a 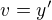 cize mame dve rovnice
cize mame dve rovnice a
a 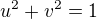 - co nas nabada prejst k polarnym suradniciam
- co nas nabada prejst k polarnym suradniciam 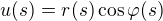 a
a  . dosadenim do druhej rovnice dostaneme
. dosadenim do druhej rovnice dostaneme 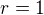 a potom z prvej rovnice dostaneme
a potom z prvej rovnice dostaneme cize
cize  teda mame
teda mame a
a  a teda
a teda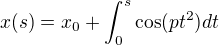 a
a 
Offline
#4 12. 03. 2015 12:32 — Editoval FliegenderZirkus (12. 03. 2015 12:33)
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Re: Odvození rovnice klotoidy
Děkuju za reakce, pomohly mi. Nakonec jsem ale přeci jen použil to běžnější odvození přes vyjádření křivosti jako derivace úhlu tečného vektoru podle parametru. Pro zajímavost posílám vlastní obrázek, jak je část klotoidy použitá jako přechodnice mezi přímou železniční tratí a kružnicovým obloukem:
Offline
#5 12. 03. 2015 16:30 — Editoval Brano (12. 03. 2015 16:36)
Re: Odvození rovnice klotoidy
to je v skutocnosti (teda aspon podla mna) to iste - cela "pointa" mala byt v tom, ze pouzijes dlzku ako parameter podla ktoreho derivujes
a potom ci uz mas krivost 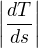 alebo
alebo  je uz tak trochu jedno (to druhe co som pouzil ja sice na prvy pohlad vyzera zbytocne komplikovanejsie, ale ma to svoje vyhody) a v tomto konkretnom pripade sa mi zda ze ked sa to rozmeni na drobne, tak je obtiaznost vypoctu rovnaka
je uz tak trochu jedno (to druhe co som pouzil ja sice na prvy pohlad vyzera zbytocne komplikovanejsie, ale ma to svoje vyhody) a v tomto konkretnom pripade sa mi zda ze ked sa to rozmeni na drobne, tak je obtiaznost vypoctu rovnaka
PS: obrazok je pekny, a preco vlastne v pouzivas klotoidu ako prechod, ma to nejake prakticke vyhody? aby dostredive zrychlenie narastalo linearne?
Offline
#6 12. 03. 2015 16:50
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Re: Odvození rovnice klotoidy
Rozumím, jj bude to nakonec velmi podobné.
Je to jak píšeš -- hlavní výhodou je odstranění nespojitosti v průběhu křivosti, a tedy i v průběhu dostředivého zrychlení. Historicky se používaly různé tvary té přechdnice, např. polynom třetího stupně. Dneska je myslím nejběžnější právě klotoida, i když existují i další modernější řešení. Druhý důvod je pak ten, že vnější kolej v oblouku bývá vůči té vnitřní vyvýšená (klopená zatáčka) a tohle vyvýšení je potřeba nějak plynule zavést, k čemuž se právě taky ta přechodnice používá.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Odvození rovnice klotoidy (TOTO TÉMA JE VYŘEŠENÉ)