Matematické Fórum

Radovan00000605 · 13. 03. 2015 15:28

Prosím vas, nepomohli by ste mi s ulohou: Najdite 2015 po sebe iducich zlozenych cisel

byk7 · 13. 03. 2015 19:29

2016! + 2, 2016! + 3, 2016! + 4, ..., 2016! + 2015, 2016! + 2016

Radovan00000605 · 13. 03. 2015 20:02

veľmi pekne ďakujem, možno je to už veľa čo chcem,ale nemohla by som sa opytat este prečo je to tak? nejake mensie odvovodnenie? Ak to uz je vela tak pochopim, aj tak dakujem :)

misaH · 13. 03. 2015 21:52 — Editoval misaH (13. 03. 2015 21:53)

↑ Radovan00000605:

Nič ti k tomu neschádza na um?

Tak si ten faktoriál trebárs rozpíš a uvedom si, čo robí to číslo, ktorého je súčasťou zloženým.

A či ozaj idú tie čísla po sebe.

Radovan00000605 · 13. 03. 2015 22:11

no ano je to tak.. rozpísala som si a zistila som, že pre každé z čisel platí 2/ n! + 2 , 3/ n!+3.........2016/ n! + 2016
Skúsila som si to pre prvých 5 zložených čisel, a každé z čísel si viem napísať ako 2(6*5*4*3 +1) , 3(6*5*4*2+1) atd.. naozaj idú po sebe. Len menšia otázka pre pochopenie , prečo to tak sedí?

Radovan00000605 · 13. 03. 2015 22:25

Alebo, ak nemám ten vztah n! +2, n!+3....atd ako ho možem odvodit? chcela by som tomu pochopi poriadne nie len niečo opísat...dakujem

byk7 · 13. 03. 2015 22:31

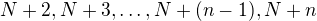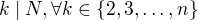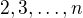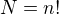K odvození, pokud chceš najít $n-1$ po sobě jdoucích složených čísel, tak chceš číslo $N$ takové, aby měla čísla $N+2,N+3,\ldots,N+(n-1),N+n$ nějakého netriviálního dělitele. Když se chvíli zamyslíš, tak dojdeš k požadavku $k\mid N,\forall k\in\{2,3,\ldots,n\}$ . Tak si řekneme, proč by $N$ nemohlo být součinem všech čísel $2,3,\ldots,n$ , tj. $N=n!$ ? Lehce nahlédneme, že v posloupnosti 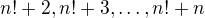$n!+2,n!+3,\ldots,n!+n$ jsou pouze čísla složená, protože všechna přípustná $k$ platí
$k+n!&=k+1\cdot2\cdot\ldots \cdot(k-1)\cdot k\cdot(k+1)\cdot\ldots\cdot(n-1)\cdot n = \\ &=k\cdot\Big(1+1\cdot2\cdot\ldots \cdot(k-1)\cdot(k+1)\cdot\ldots\cdot(n-1)\cdot n\Big)$

Číslo $k+n!$ je tak součinem dvou čísel větších než jedna, což znamená, že to nemůže být prvočíslo pro žádné $k\in\{2,3,\ldots,n\}$ .