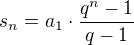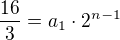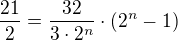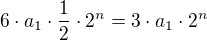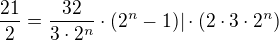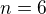Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#4 15. 03. 2015 15:27
Re: geometrická postupnosť
↑ gadgetka:
Ahoj a prečo tam je 32= 3a1 * 2^n lebo nerozumiem a ako to mam dalej upravovať? :)
Offline
#5 15. 03. 2015 15:28 — Editoval gadgetka (15. 03. 2015 15:31)
Re: geometrická postupnosť
Celou rovnici jsem vynásobila šesti, abych se zbavila zlomku. :)
Edit: A v závěru opět celou rovnici vynásob společným jmenovatelem  a třicítkou dvojkou roznásob závorku
a třicítkou dvojkou roznásob závorku  .
.
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#7 21. 06. 2015 00:53
Re: geometrická postupnosť
↑ fransiz:
Tak to nechápu ...
když rovnici  vynásobím 6tkou tak snad dostanu
vynásobím 6tkou tak snad dostanu 
Proč tam je uvedeno  ? sem mimo o.O :D
? sem mimo o.O :D
Offline
#9 21. 06. 2015 05:59
Re: geometrická postupnosť
↑ gadgetka:
Děkuju =)
---------------------
Pro ty kdo by potřeboval pokračovat dál a nevěděl si rady, louskal jsem to déle :D
Řešení po tom co jsme našli a1 a dosadíme do rovnice pro sn
1) 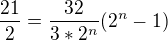
2) 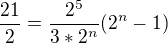 -> Stejný základ pro vzorec
-> Stejný základ pro vzorec 
3) 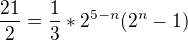
4)  -> Použijeme vzorec
-> Použijeme vzorec 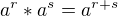
5) 
6)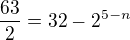 převedeme zpět
převedeme zpět 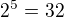
7)  - izulujeme si N
- izulujeme si N
8)  vynásobime -1 rovnici
vynásobime -1 rovnici
9) 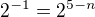 Podle vzorce
Podle vzorce 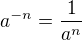
10) A podle stejného základu máme jasný výsledek n=6
-----------------------------
Pokud je někde chyba tak sorry opisoval jsem to ze sešitu :D
Offline