Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 17. 03. 2015 14:56
- vulkan66


- Místo: Praha
- Příspěvky: 416
- Škola: ČVUT FJFI - Částicová fyzika
- Pozice: student
- Reputace: 20
Re: Vektory lineárně nezávislé
Ano, až na to, že nulový vektor má být ve sloupci pravých stran. Nebo nejlépe se nemusí psát vůbec.
Vím, jak ovládat vesmír. Tak mi řekněte, proč bych se měl hnát za milionem? -Grigorij Perelman
Offline
#3 17. 03. 2015 15:24
Re: Vektory lineárně nezávislé
Ahoj ↑ maver:,
Doplnujem prispevok od kolegu ↑ vulkan66:.
Co planujes robit z najdenou maticou?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 17. 03. 2015 17:54
Re: Vektory lineárně nezávislé
↑ maver:
Ano, cize mas nast vsetki take a, pre ktore rovnica 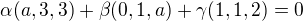 co si napisal, ma jedinne riesenie
co si napisal, ma jedinne riesenie 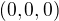 .
.
Cize mozes zasa pouzit GEM.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 18. 03. 2015 20:59
Re: Vektory lineárně nezávislé
↑ vanok:
nyní by mě zajímala strategie při hledání "a" pomocí GEM: musím opět dostat jeden řádek samé nuly kromě jednoho sloupce, kde bude nějaká rovnice s parametrem "a" - a ta rovnice, když bude rovna nule, to znamená, že pro toto "a" jsou vektory lineárně nezávislé?
Offline
#7 19. 03. 2015 11:35 — Editoval vanok (19. 03. 2015 11:38)
Re: Vektory lineárně nezávislé
Ahoj ↑ maver:,
To mas pravdu, ze tu je treba mat trochu zvyk z riesenim rovnice metodou GEM. Lebo ak pri postupe budes delit z nejakym koeficientom co obsahuje parameter a, budes musi et potom urobit diskuziu tykajucu sa toho delenia.
Tu napr. 
Je vyhodne najprv urobit r3-->r3--r2 ( pisem operacie skratene ako je to zvykom, ale pre prehladnost len jednu operaciu naraz )
Teraz r1<-->r2 (vymena r1 a r2) 
r1-->r1/3
r2-->r2- a r1
r2-->-\frac 3a r2
Skus to dokoncit... Ostavaju 2 etapy a diskuzia z a. A pochopitelne konkluzia.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 19. 03. 2015 17:45
- vulkan66


- Místo: Praha
- Příspěvky: 416
- Škola: ČVUT FJFI - Částicová fyzika
- Pozice: student
- Reputace: 20
Re: Vektory lineárně nezávislé
Řekl bych, že by ta matice šla upravit lépe. Já si nejdřív dal na první místo vektor (1,1,2) a výsledná matice mi vyšla
(snad je to dobře :) )
Teď zbývá určit pro jaký parametr má matice maximální hodnost.
Vím, jak ovládat vesmír. Tak mi řekněte, proč bych se měl hnát za milionem? -Grigorij Perelman
Offline
#10 19. 03. 2015 18:49
Re: Vektory lineárně nezávislé
↑ vulkan66:
je to správně.
To je další věc, kterou nevím: v učebnici máme právě toto vulkan66ovo řešení:
1 1 2
0 1 a
a 3 3
Vektory jsou LN a pro to platí formule, kterou jsem napsal 
v tom druhém řešení jsou vektory psány pod sebou. Která věta toto umožňuje?
Pokračuji: pokud 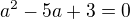 budou v posledním řádku samé nuly pro
budou v posledním řádku samé nuly pro 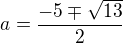
zbývá nám matice
protože ve zbylých řádcích nejsou samé nuly, vektory jsou pro toto "a" LZ.
Potud chápu. V učebnici ale máme, že pro jiná, než toto "a" jsou vektory LN - to nechápu: když dám a=0, pak nejsou všude 0 a proto si nesprávně myslím, že i tak budou vektory LZ.
PS: poznám LN vektor z matice tak, že jeden řádek jsou všude 0? Nebo musí být 0 na všech řádcích (kromě jednoho)?
Offline
#11 19. 03. 2015 20:16 — Editoval vulkan66 (19. 03. 2015 20:17)
- vulkan66


- Místo: Praha
- Příspěvky: 416
- Škola: ČVUT FJFI - Částicová fyzika
- Pozice: student
- Reputace: 20
Re: Vektory lineárně nezávislé
↑ maver:
Nejsem si jistý, jestli je na to nějaká věta. Já to také vidět několikrát psané do řádků (myslím, že v nějakém textu MFF).
Zbytečně to komplikuješ. Pokud je hodnost matice maximální (všechny sloupce jsou hlavní) nelze vytvořit netriviální lin. kombinaci -> LN. Pokud bude nějaký sloupec vedlejší, lze ho nakombinovat pomocí ostatních -> LZ.
Podstatné pro, to jestli jsou sloupce vedlejší nebo hlavní jsou čísla na hlavní diagonále. Pro tebe je to pouze poslední člen vpravo. Pokud bude to číslo 0, hodnost matice = 2 -> LZ. Pokud bude nenulové, hodnost matice = 3 -> LN
Vím, jak ovládat vesmír. Tak mi řekněte, proč bych se měl hnát za milionem? -Grigorij Perelman
Offline
#12 19. 03. 2015 21:11 — Editoval vanok (19. 03. 2015 22:23)
Re: Vektory lineárně nezávislé
Ahoj ↑ vulkan66:,
Ak si pozozne cital, tak som napisal ze treba urobit este dve upravy na ukoncenie triagularizacie.
Upravy z prezantaciou co som napisal, maju pedagogicky ciel
...
Tvoja, moja, a lubovolna ina platna metoda daju ti istu odpoved.
Cize ziadna nie je lepsia ako ina. Ale co je dolezite je prist k spravnezapis vysledku.
↑ maver:
Co pises nie je celkom presne.
Tvoja matica, ktoru si napisal ako matice rozsireneho lin. systemu vyhovuje vtedy, ked ukazes ze ma hodnost 3.
Pre dve "a"co si nasiel, jej hodnost je 2. Preto vsetki "a" az na tie dva co si vyjadrit vyhovuju.
Veta o ktorej hovoris pracovat na riadkoch alebo stlpcoch je dosledok toho, ze hodnost matice a jej trasponovanej matice su rovnake.
↑ vulkan66:
Tvojej poznamke o vedlajsich stlpcoch nerozumiem, lebo ide o nestandartnu termiminogiu.
Poznamka.Su aj ine metody, no kolega chcel pracovat na maticach a vyriesit ,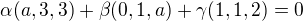 , tak jedna dobra metoda je GEM.
, tak jedna dobra metoda je GEM.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#13 19. 03. 2015 21:37
- vulkan66


- Místo: Praha
- Příspěvky: 416
- Škola: ČVUT FJFI - Částicová fyzika
- Pozice: student
- Reputace: 20
Re: Vektory lineárně nezávislé
vanok napsal(a):
Cize ziadna nie je lepsia ako ina. Ale co je dolezite je prist k spravnezapis vysledku.
Ok, ty si to klidně dělej složitě, ale někdo by to rád udělal lehce. V praxi se prostě dává nejjednodušší sloupec na první místo, tak nevím, o čem to mluvíš.
Jo a prosím vysvětli mi, čemu nerozumíš. Podle mě je to zcela standartní terminologie, tak mi to vysvětli.
Vím, jak ovládat vesmír. Tak mi řekněte, proč bych se měl hnát za milionem? -Grigorij Perelman
Offline
#14 19. 03. 2015 22:20
Re: Vektory lineárně nezávislé
↑ vulkan66:,
Prajem ti vela uspechov.
Dobre pokracovanie.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#15 19. 03. 2015 23:31 — Editoval maver (20. 03. 2015 00:03)
Re: Vektory lineárně nezávislé
Takže odnáším si z naší diskuse řešení matic s parametrem toto:
když řeším to, zda jsou vektory LN či LZ a mám matici s parametrem, tak:
a) je jedno, jestli nanáším svisle nebo vodorovně (viz poznámka o hodnotě transpozonové matice totožné s maticí původní).
b) nejprve si upravím matici a zjistím její hodnotu.
I. Pokud počet řádků matice před i po úpravě zůstává stejný (hodnota se nemění, jde o regulární matici), pak vektory jsou LN.
II. Pokud nejde o regulární matici (=h(A)<n), vektory jsou LZ.
Interpretace výsledku: Při detailním pohledu na strukturu matice, zkoumám poslední řádek, kde jsou na posledním řádku GEM úprav ve všech pozicích nuly, kromě jedné, kde mám parametr. Pokud je funkce tohoto parametru = 0, pak dokazuji, že h(A) <n (řádek s nulami vymažu a tím se sníží hodnotamatice z n na n-1) a tudíž odpověď je, že pro tento parametr "a" jsou vektory LZ viz b) II. Pokud funkce tohoto parametru je různá od nuly, hodnota matice zůstává a vektory jsou LN viz b) I.
PS: Jen zde mám doplňující dotaz: viděl jsem podobný příklad, kde se zkoumalo, zda je vektor součástí obalu, ve kterém byly další tři vektory. A mě podivilo, že autor skript zde nejprve zkoumal LZ/LN těch vektorů uvnitř obalu - zde vypočítal, že h(A) =n, dokázal, že vektory jsou LN a pak pokračoval s takto upravenou maticí, kde přiložil neznámý vektor. Můj dotaz je: šlo by vynechat tento postup a rovnou udělat matici s mixem všech vektorů = jak těch uvnitř obalu, tak i ten neznámý?
Offline
#16 19. 03. 2015 23:43 — Editoval vanok (19. 03. 2015 23:45)
Re: Vektory lineárně nezávislé
↑ maver:,
Mas dobru syntezu prace, tu klucove slovo bolo hodnost 3.... A viacej postupov ako to riesit.
Co sa tyka obalu. Popisana metoda je rozumna, lebo najprv autor iste chcel najst bazu obalu.
Potom je jednoduche posudit ci zvysny vektor je alebo nie je v obale.
Inac, vo vseobecnom pripade by nemohol to vediet.
Tvoja interpretacia plati v pripade stvorcovych matic. Inac to je trochu koplikovanejsie.
Dobre pokracovanie.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#17 19. 03. 2015 23:59 — Editoval maver (20. 03. 2015 00:00)
Re: Vektory lineárně nezávislé
↑ vanok:
néééééééééé, já myslel, že je to pro všechny matice. To mě picne teda.
Moment - pokud ale budu nanášet vektory do matice klasicky (svisle), tak by to mělo být univerzální, ne? Takže jen ten bod a) platí pro (n,n), ne? Zbytek je univerzál ne?...
A dále: když ten autor vypočítal, že vektory uvnitř obalu byly v LN a tudíž tvořily bázi, pak stejně k té GEM upravené matici připíchnul vodorovně zkoumaný vektor a zde přišel zajímavý moment: na základě stejného postupu (funkce s "a" parametrem=0) a místo toho, aby řekl: pro toto "a" je vektor LZ s ostatními, řekl: vektor je součástí obalu. A to mě mate. Na jedné straně původní vektory v obalu byly LN, ale testovaný vektor byl LZ a současně součástí obalu?
Offline
#18 20. 03. 2015 00:14 — Editoval vanok (20. 03. 2015 00:27)
Re: Vektory lineárně nezávislé
↑ maver:
Obal prave to overene, vo vseobecnej situacii, vektor LZ je v ovale , LN nie je v obale.
Co sa tykalo poslednej matice z "a" tam islo pre tie zle"à" o nulovy riadok.
Pozor, ak sa daju do matice vektory zvislo , tak to ti neumozni riesenie rovnice, ako tej co si napisal v prvom prispevku...ale pre hodnost matice to je platne.
V tvojom cviceni ano.
Mas 3 vektory typu (.,.,.)
Ale vseobecne mozes mat napr. 3 vektory typu (. , . ,. ,. ) co da inu konfiguraciu ( ale metoda prace moze byt ta ista)
Ak si chces po citat o hodnosti, pozri si napr. toto
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline