Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Definiční obory - je to dobře? :o) (TOTO TÉMA JE VYŘEŠENÉ)
#2 19. 03. 2009 20:19 — Editoval O.o (19. 03. 2009 20:20)
Re: Definiční obory - je to dobře? :o)
↑ Zbyšek:
Ty prvé vypadají snad správně, ale neověřoval jsem to. K tomu třetímu, mohl bys prosím doplnit složené závorky, aby bylo jasné, kde je odmocnina a jak přesně vypadá zlomek?
Děkuji ;.-)
PS: U toho druhého nejsou kulaté závorky, protože pod odmocinou může být i nula ;-)
Offline
#4 19. 03. 2009 20:24
- marnes

- Příspěvky: 11227
Re: Definiční obory - je to dobře? :o)
↑ Zbyšek:1) i 2) jsou v pořádku, včetně kulatých závorek. Je pravda, že pod odmocninou být nula může, ale ne ve jmenovateli. Takže OK. U trojky nevidím podmínky žádné. Ani zlomek, ani odmocnina, ani funkce
Jo. A na začátku vás zdravím.
Offline
#5 19. 03. 2009 20:26 — Editoval O.o (19. 03. 2009 20:33)
Re: Definiční obory - je to dobře? :o)
↑ halogan:
↑ marnes:
Stydím se, nějak jsem zapoměl, že jde o zlomek .-).
PS: Klikněte si an poslední příklad, aby se vám zobrazil jeho texový přepis ;-).
Čekal bych něco takového: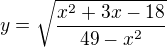
Což by se asi dalo řešit nějak takto (?):
Jsem unavený, tak snad jsem znovu někde nevyskošil s nějakou hloupostí ;)
Offline
#10 19. 03. 2009 20:47 — Editoval marnes (19. 03. 2009 20:49)
- marnes

- Příspěvky: 11227
Re: Definiční obory - je to dobře? :o)
↑ Zbyšek:
3) zlomek pod odmocninou musí být větší nebo roven jak nula
- čitatel lze rozložit na (x+6).(x-3)
jmenovatel na(7-x).(7+x)
máme 4 nulové body, sestavíme, jak bylo doporučeno tabulku nulových bodů
- mě vyšlo, že jedefiniční obor (mínus nekonečno;-7) sjed /-6;3/ sjed (7;nekonečno) "/ "- uzavřeno
Jo. A na začátku vás zdravím.
Offline
#13 19. 03. 2009 21:41
Re: Definiční obory - je to dobře? :o)
↑ marnes:
Jé děkuji, zrovna v tomhle nejsem moc dobrý, ale snažím se s tím něco dělat, jen zapomněl a rozuměl, tam se mi to dost plete.
PS: Smekat nad tím, co umím? Není nad čím, myslíš, že zrovna ty máš daleko větší rozsah, což je vidět hned po připojení, když téměř všechna témata končí tvými radami ;-)
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » Definiční obory - je to dobře? :o) (TOTO TÉMA JE VYŘEŠENÉ)