Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 23. 03. 2015 14:57
Re: Lin algebra - permutace
Ahoj ↑ maver:,
Daj mi anglicky alebo francuzky nazov tvojho pojmu, a tiez jeho definiciu.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 23. 03. 2015 15:40
Re: Lin algebra - permutace
Konverzia
To je kto?co?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 23. 03. 2015 16:46
Re: Lin algebra - permutace
Pokial nevieme co je  ,tak sa tomu neda rozumiet.
,tak sa tomu neda rozumiet.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 23. 03. 2015 17:36
Re: Lin algebra - permutace
↑ maver:,
Aha, teraz to rozumiem.
Ide o permutaciu 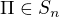 , taku ze
, taku ze  .
.
Ked pouzijes definiciu inverzie jednej permutacie, co som pripomenul v predoslom cviceni, tak odpoved je 0 ( nula).
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#10 23. 03. 2015 21:15
Re: Lin algebra - permutace
Sn= to je groupa permutacii na mnozine { 1,2,3,...,n}
Je cislo z tej mnoziny Je obraz 1 cisla k vdaka permutacii z
Je obraz 1 cisla k vdaka permutacii z 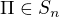
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
