Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Stereometrie - objemy a povrchy těles (TOTO TÉMA JE VYŘEŠENÉ)
#1 17. 01. 2014 19:30
Stereometrie - objemy a povrchy těles
Dobrý večer, ve škole počítáme povrchy a objemy koule a narazila jsem na příklad, u kterého nevím, jak na něj.
Krychli opište a vepište kouli. Vypočítejte poměr objemů koule opsané, krychle a koule vepsané.
Předem děkuji za rady:)
Offline
- (téma jako vyřešené označil(a) janca361)
#2 17. 01. 2014 19:41
- Peterslovak

- Příspěvky: 270
- Škola: gymnázium
- Pozice: student
- Reputace: 3
Re: Stereometrie - objemy a povrchy těles

pí mi nešlo zapsat, ale víš co to je
„Představivost je důležitější než vědomosti.“- Albert Einstein
Offline
#3 17. 01. 2014 19:43
Re: Stereometrie - objemy a povrchy těles
Objem krychle: 
Objem koule opsané = poloměr se rovná polovině tělesové uhlopříčky = 
Objem koule vepsané = poloměr se rovná polovině strany = 
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#5 17. 01. 2014 19:53
Re: Stereometrie - objemy a povrchy těles

Krychle je ke kouli opsané v tomto poměru:
Krychle je kouli vepsané v tomto poměru.
Když upravíš první výsledek máš:
Takže u obojího máš šestku u krychle. Takže můžeš psát poměr:
Krychle : koule vepsaná : koule opsaná = 
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » Stereometrie - objemy a povrchy těles (TOTO TÉMA JE VYŘEŠENÉ)

 :/
:/ vyjde 3.a
vyjde 3.a .
.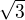 dekuji za odpoved
dekuji za odpoved