Matematické Fórum

Mythic · 25. 03. 2015 23:12

Chci se optat, proč platí věta:

"Hodnost transponované matice je stejná jako hodnost původní matice."

Z několika zdrojů jsem jí takto našel, nikde však nebyla dokázaná a mě nedává smysl.

Např. u matice:

//forum.matweb.cz/upload3/img/2015-03/21506_Sn%25C3%25ADmek%2Bobrazovky%2B2015-03-25%2Bv%25C2%25A023.11.15.png

to urcite neplati.

Jak to tedy je?

Al1 · 26. 03. 2015 08:01

Hodnost matice udává počet všech různých lineárně nezávislých vektorů (řádků). V transponované matici k matici A ti při řádkové úpravě na trojúhelníkovou matici vyjdou dva stejné řádky (jsou lineárně závislé), jeden vynecháš a hodnost transponované matice bude také 2 jako u A.
http://www.slu.cz/math/cz/knihovna/docs … niova-veta

vulkan66 · 26. 03. 2015 09:57

V každých skriptech lineární algebry by tato věta měla být dokázána.

Rumburak

↑ Mythic:

V podstatě jde o větu, která říká, že je-li dána matice $A$ , pak lineární obal jejích řádků a lineární obal jejích sloupců
mají tutéž dimensi.

Nechť $m$ je počet jejích řádků a $n$ počet jejích sloupců. To znamená, že pro libovolný "sloupcový" vektor $\vec{x} \in \mathbb{R}^n$
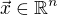
je definován součin 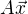$A\vec{x}$ , výsledkem kteréžto operace je "sloupcový" vektor v $\mathbb{R}^m$ .

Předpisem $f : \vec{x} \mapsto A\vec{x}$ je pak definováno lineární zobrazení (neboli homomorfismus) prostoru $\mathbb{R}^n$ do $\mathbb{R}^m$ .
Podle známé věty z lin. algebry platí

$\dim (\text{Ker}(f)) + \dim (\text{Im}(f)) = \dim(\mathbb{R}^n) = n$ ,

kde $\text{Ker}(f)$ je jádro homomorfismu $f$ (množina těch vektorů, jejichž obrazem je nulový vektor) a $\text{Im}(f)$ obor
jeho hodnot. Je zřejmé, že $\text{Im}(f)$ je totožný s lin. obalem sloupců matice $A$ , zatímco $\text{Ker}(f)$ je ortogonálním
doplňkem k lin. obalu řádků matice $A$ .

Dokončení důkazu možná už zvládneš. :-)

Pokud jde o matici z Tvého úvodního příspěvku:

Její dva řádky jsou lineárně nezávislé, takže její "řádková" hodnost je 2 .
Její první dva sloupce jsou rovněž lin. nezávislé, takže "sloupcová" hodnost je nejméně 2. Větší než 2 ale být nemůže,
protože lin. obal sloupců je podprostorem v 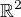$\mathbb{R}^2$ , jehož dimense je 2.