Matematické Fórum

Nia · 03. 04. 2015 00:16 — Editoval Nia (03. 04. 2015 00:20)

Ahoj, ráda bych Vás poprosila o radu s jedním integrálem. Mám ho dokonce i spočítaný, jen bych se chtěla zeptat na radu, proč nemůžu udělat jednu matematickou operaci.

1. způsob (je správně):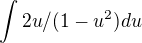

$\int {2u}/({1-u^{2}}) du$

substituce t = 1-u^2
dt = -2u du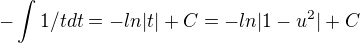

$-\int {1}/{t}dt = -ln |t|+C=-ln|1-u^{2}|+C$

2. způsob - proč je špatně?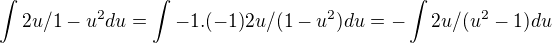

$\int {2u}/{1-u^{2}}du =\int {-1}.{(-1)} {2u}/({1-u^{2}})du =-\int {2u}/({u^{2}-1})du$

substituce t = u^2-1
dt = 2u du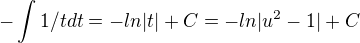
$-\int {1}/{t}dt = -ln |t|+C=-ln|u^{2}-1|+C$

možná namítnete, že jsou to totožné výsledky, protože výraz je v absolutní hodnotě, ale přesto si nemyslím, že v to je ten problém
díky za pomoc!

byk7 · 03. 04. 2015 00:20

Proč by měl být špatně?

Freedy · 03. 04. 2015 00:22

Ahoj,

zkus si sám odvodit, proč platí: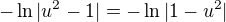
$-\ln |u^2-1|=-\ln |1-u^2|$
víceméně, stačí si odvodit proč platí: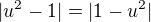
$|u^2-1|=|1-u^2|$ (nápověda: na obou stranách máš kladné číslo, proto je umocnění obou stran ekvivalentní úprava, sám se přesvědč, zda-li po umocnění nastane rovnost :) )

Nia · 03. 04. 2015 00:42 — Editoval Nia (03. 04. 2015 00:48)

díky za odpověď
nicméně já si uvědomuju, že ty výrazy se rovnají, proto jsem na konci psala o té absolutní hodnotě

tenhle integrál je dílčím krokem v řešení jedné deferenciální rovnici a jakmile výrazy odlogaritmuju a vyruším i absolutní hodnoty, tak se výsledek samozřejmě změní.. to mě mate

ale jsem ráda, že vím, že ten druhý způsob výpočtu je ok: )

Matematické Fórum

#1 03. 04. 2015 00:16 — Editoval Nia (03. 04. 2015 00:20)

integral

#2 03. 04. 2015 00:20

Re: integral

#3 03. 04. 2015 00:22

Re: integral

#4 03. 04. 2015 00:42 — Editoval Nia (03. 04. 2015 00:48)

Re: integral

Zápatí