Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Numerické řešení soustavy diferencíálních rovnic
#1 02. 04. 2015 13:37 — Editoval nouma1 (02. 04. 2015 13:38)
Numerické řešení soustavy diferencíálních rovnic
Ahoj dokáže mi někdo poradit jakými numerickými (matematickými) metodami se dá vyřešit tato soustava diferenciálních rovnic? Potřebuji k tomu více metod abych mohl srovnávat.
Hledal jsem zda jsou to obyčejné diferenciální rovnice - s poč podminkama nebo obyčejné diferenciální rovnice - okrajové ulohy nebo parciální dif. rovnice. ALe nedokážu posoudit o jaký typ jde.
Offline
#2 02. 04. 2015 14:12 — Editoval Rumburak (02. 04. 2015 14:15)
Re: Numerické řešení soustavy diferencíálních rovnic
↑ nouma1:
Ahoj.
Jen pokud jde o tu klasifikaci typu:
Jde o soustavu obyčejných dif. rovnic . Neznámými jsou funkce  proměnné
proměnné  .
.
Rovnice jsou druhého řádu a nelineární.
Počáteční ani okrajové podmínky zadány nejsou, avšak u numerických metod se bez nich neobejdeme,
pokud vím.
Offline
#3 02. 04. 2015 14:22
Re: Numerické řešení soustavy diferencíálních rovnic
↑ Rumburak:
Ok super . Učitel mi poradil od Vitáska-Numerické metody.
No hledám v tom a nic moc. A dokážeš mi říct aspon nějakou metodu jakou se to dá matematicky řešit?.
Ano jak říkáš z neznámými souhlasím a s proměnou čas také.
Offline
#4 02. 04. 2015 14:39 — Editoval Rumburak (02. 04. 2015 14:52)
Re: Numerické řešení soustavy diferencíálních rovnic
↑ nouma1:
Bohužel o numerických metodách mám jen velmi vágní povědomí. Poradím nejvýše některé názvy, které mi uvízly
v paměti, aniž bych dovedl odhadnout, zda se příslušná metoda pro tento problém vůbec hodí.
- metoda Eulerova,
- metoda konečných prvků ,
- metoda Runge-Kuttova ,
...
snad někdo další doplní, opraví, případně nasměruje .
Offline
#5 02. 04. 2015 14:42
Re: Numerické řešení soustavy diferencíálních rovnic
↑ Rumburak:
Doufám v to zatím děkuji. Jde mi to ze mam jen nastnit problematiku toho typu (soustavy) jak by se to dalo řešit (jakými num. metodami) kdyz mi nekdo nahodí aspoň pár metod budu jen rád a ja už si s tím nějak poradím. :)
Offline
#7 02. 04. 2015 15:07 — Editoval nouma1 (02. 04. 2015 15:08)
Re: Numerické řešení soustavy diferencíálních rovnic
↑ Rumburak:
Numerika
Myslíš tyto metody? Tedy od strany 107 .?
Offline
#10 02. 04. 2015 17:43
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Re: Numerické řešení soustavy diferencíálních rovnic
Zdravím,
jak píše ↑ Rumburak:, je potřeba znát počáteční podmínky. Jelikož je nezávisle proměnnou čas, lze předpokládat, že budeme znát hodnotu neznámých  a jejich prvních derivací podle času pro nějaký čas
a jejich prvních derivací podle času pro nějaký čas 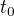 . To je obvykle jednodušší úloha než kdyby nezávisle proměnnou byla poloha a hodnoty řešení a prvních derivací byly předepsány v různých bodech. Pak bychom hovořili o okrajových podmínkách.
. To je obvykle jednodušší úloha než kdyby nezávisle proměnnou byla poloha a hodnoty řešení a prvních derivací byly předepsány v různých bodech. Pak bychom hovořili o okrajových podmínkách.
Řada numerických metod pracuje pouze se soustavami rovnic prvního řádu. Pokud budeš ten řešič i sám programovat (ano nebo ne?), tak bys nejspíš začal přepisem té soustavy dvou rovnic druhého řádu na soustavu čtyř rovnic prvního řádu.
U tvojí soustavy bude největší výzvou nespojitost funkce signum. Určitě o tomhle tématu ale najdeš spostu článků či alspoň diskuzí, např.
Odkaz 1
Odkaz 2
Offline
#11 02. 04. 2015 18:42 — Editoval nouma1 (03. 04. 2015 16:32)
Re: Numerické řešení soustavy diferencíálních rovnic
↑ FliegenderZirkus:
Ne nebudu to řešit jen mám nastudovat mozné numerické metody kterými se to dá řešit.
Jen nastínení (to je vyjmenovat mozné metody, trochu je popsat a zhodnotit je, jaka je na co lepší atd..)
Jde mi jen o teorii. Nevím zda to lze považovat za mozné počáteční podmínky. Ale je to uloha tedy rovnice simulujici inv. kyvadlo. Mužeme do toho zahrnout počátční uhel 0 a poloha muže bzt taky stanovena (poloha voziku)(druhe derivace tedy rychlost vozíku v počátku =0 a uhlové zrychleni je taky 0).
K tomu mi snad bude stačit výše zmíněný odkaz.
Moje otázka zní :Bude mě tedy zajimat num řešeni obyčejných dif rovnic -ulohy s počátečnímy podmínkami nebo num. řešeni dif. rovnic -okrajové úlohy?
Offline
#13 03. 04. 2015 18:29
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Re: Numerické řešení soustavy diferencíálních rovnic
Mužeme do toho zahrnout počátční uhel 0 a poloha muže bzt taky stanovena (poloha voziku)(druhe derivace tedy rychlost vozíku v počátku =0 a uhlové zrychleni je taky 0).
Ono je to právě trochu jinak, počáteční úhel a polohu stanovit musíme, nikoli jen můžeme. To samé platí o jejich prvních derivacích podle času. Pokud totiž ne, tak žádný numerický řešit ani nenastartujeme. Jiná otázka by byla, pokud bychom se na ty rovnice dívali čistě matematicky a hledali všechna možná řešení v závislosti na různých počátečních podmínkách. To ale myslím není tvůj případ.
Ještě k té terminologii - o druhé derivaci polohy podle času se vyjadřuješ jako o rychlosti, ačkoli se jedná o zrychlení, ale to bude nejspíš jen překlep.
Druhé derivace neznámých v počátečním čase se spočítají po dosazení nultých a prvních derivací do pohybových rovnic, bude to soustava dvou lineárních rovnic pro dvě neznámé.
Ještě k těchrovnicím - nemám sice obrázek té soustavy, ale jestliže je rameno upevněno na vozíku, neměla by se jeho hmotnost taky počítat do třecí síly?
Rozdíl mezi okrajovými a počátečními podmínkami už by v tuto chvíli měl být zřejmý, nebo ne?
Offline
#14 03. 04. 2015 18:37 — Editoval nouma1 (03. 04. 2015 18:40)
Re: Numerické řešení soustavy diferencíálních rovnic
↑ FliegenderZirkus:
Ano jedná se o překlep x je poloha ,1 derivace rychlost ,2 derivace zrychleni
K rovnicím- ano míš zcela pravdu - hmotnost ramene je proti voziku 1/10 ..takze sem ji zatím zanedbal
Takže pokud to chápu tak se jedná o soustavy s poč. podminkamí
našel jsem tyto: eulerova metoda, ExplicitníRungovy-Kuttovy metoda, Linearní mnohokrokové metody a tuhé metody. Snad jsem to pochopil správně.
Tedy postup : převest na dif. prvního řádu a nasledn vyuzit nejakou z techto metod :)?
Offline
#15 03. 04. 2015 18:44
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Re: Numerické řešení soustavy diferencíálních rovnic
↑ nouma1:
Ano myslím že jsi na správné cestě. K úplnosti či vhodnosti seznamu se moc vyjadřovat nemůžu, ale třeba ta skupina metod Runge-Kutta je velmi rozšířená a ve spoustě případů by to asi byl takový první pokus co vyzkoušet.
Offline
#16 03. 04. 2015 18:47 Příspěvek uživatele nouma1 byl skryt uživatelem nouma1. Důvod: navic info
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Numerické řešení soustavy diferencíálních rovnic