Matematické Fórum

kucape · 10. 04. 2015 18:13

Zdravím,
potřeboval bych poradit s postupem.

Mám zadání:

Najděte všechny lokální extrémy funkce f dané předpisem $f(x) = \sin x +\cos x$

Derivace:
$f'(x) = \cos x -\sin x$

Nalezení bodů podezřelých z extrému:

$\cos x -\sin x=0$
$\cos x =\sin x$

$x_{1}=\frac{\pi }{4}+2k\pi$
$x_{2}=\frac{5\pi }{4}+2k\pi$

Když si to načrtnu do jednotkové kružnice:

//forum.matweb.cz/upload3/img/2015-04/82261_kruznice1.png

Jak mám tedka vyšetřit ty intervaly kdy je derivace kladná nebo záporná ? Mám tam brát v potaz i nulové body sinu a cosinu ?

Al1 · 10. 04. 2015 18:41

↑ kucape:

Zkus si třeba načrtnout grafy $y=\sin x$ a $y=\cos x$ do jedné soustavy souřadnic a zkoumej, kdy je $\cos x>\sin x$ (v daných intervalech je pak fce rostoucí), nebo $\cos x<\sin x$ (fce klesající). V nulový bodech $\frac{\pi }{4}+k\pi$ jsou průsečíky obou grafů.

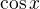Nebo sleduj na jednotkové kružnici nabývání a klesání hodnot $\sin x$ (jsou na ose y) a $\cos x$ (jsou na ose x).
V nulových bodech první derivace pak hledáme extrémy fce.

kucape · 10. 04. 2015 21:29

//forum.matweb.cz/upload3/img/2015-04/92800_graf1_up.png

Takže fce:

roste na intervalu $\langle\frac{-3\pi }{4}+2k\pi;\frac{\pi }{4}+2k\pi \rangle$ (tady si nejsem jisty jestli jsem to vypočital správně)

klesa na intervalu $\langle\frac{\pi }{4}+2k\pi;\frac{5\pi }{4}+2k\pi \rangle$

roste na intervalu $\langle\frac{5\pi }{4}+2k\pi;\frac{9\pi }{4}+2k\pi \rangle$

A z toho vyplývá že má v $\frac{\pi }{4}+2k\pi$ lokální maximum, a v $\frac{5\pi }{4}+2k\pi$ lokální minimum.

Je to správně?

Al1 · 10. 04. 2015 21:55

↑ kucape:

Je to dobře, jen bych napsal pouze jeden interval pro fci rostoucí, stačí $(\frac{-3\pi }{4}+2k\pi;\frac{\pi }{4}+2k\pi )$ , neboť ten další $(\frac{5\pi }{4}+2k\pi;\frac{9\pi }{4}+2k\pi )$ je pouze jeho jiným vyjádřením (dej k=1 do předchozího a máš tento), intervaly jsou otevřené dle podmínek definice rostoucí či klesající fce pomocí derivace.

Extrémy souhlasí, lokál.max. $\bigg[\frac{\pi }{4}+2k\pi ;\sqrt{2}\bigg]$ , lokál. min. $\bigg[\frac{-3\pi }{4}+2k\pi ;-\sqrt{2}\bigg]$

kucape · 10. 04. 2015 22:19

↑ Al1:

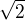Dobře, děkuji, jenom bych se ještě zeptal co znamená presně ten středník a $\sqrt{2}$ , jak jste psal $\bigg[\frac{\pi }{4}+2k\pi ;\sqrt{2}\bigg]$ ?

Al1 · 10. 04. 2015 22:26

↑ kucape:

$\bigg[\frac{\pi }{4}+2k\pi;\sqrt{2}\bigg]$ jsou všechna lokální maxima, kdy $x=\frac{\pi }{4}+2k\pi$ a $y=\sqrt{2}$

Tedy pokud do předpisu fce zadáme $x=\frac{\pi }{4}+2k\pi$ , vypočítáme $y=\sqrt{2}$

kucape · 10. 04. 2015 23:20

↑ Al1:

Aha, už rozumím. Díky moc :)

Matematické Fórum

#1 10. 04. 2015 18:13

Nalezení lokálních extrému

#2 10. 04. 2015 18:41

Re: Nalezení lokálních extrému

#3 10. 04. 2015 21:29

Re: Nalezení lokálních extrému

#4 10. 04. 2015 21:55

Re: Nalezení lokálních extrému

#5 10. 04. 2015 22:19

Re: Nalezení lokálních extrému

#6 10. 04. 2015 22:26

Re: Nalezení lokálních extrému

#7 10. 04. 2015 23:20

Re: Nalezení lokálních extrému

Zápatí