Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#4 11. 04. 2015 20:13 Příspěvek uživatele EvBes byl skryt uživatelem EvBes. Důvod: nalezena chyba
#9 12. 04. 2015 11:24
Re: Odchylka asymptot
Ahoj ↑ Al1:,
Pozor ide o skalarny sucin, a nie o vektorovy sucin.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#11 12. 04. 2015 12:28
Re: Odchylka asymptot
↑ Al1: ,
Ok, vsak preklep sa stane kazdemu.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
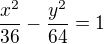
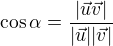
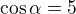 a tím pádem mi prostě ten úhel nevyjde.. :/ kde dělám chybu? Děkuji
a tím pádem mi prostě ten úhel nevyjde.. :/ kde dělám chybu? Děkuji
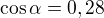 .
.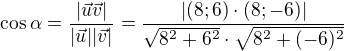
 je 1 :/. A vám vyšlo 0.28
je 1 :/. A vám vyšlo 0.28
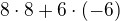 .
.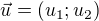
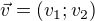 ,
,