Matematické Fórum

EvBes · 12. 04. 2015 00:28

Zdravím,
bohužel si nevím rady s příkladem:
Je dán čtyřstěn s vrcholy A[3;5;3] B[-2;11;-5] C[1;-1;4] D [0;6;4]. Určete výšku 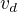$v_{d}$ .

Zkoušela jsem to tak,že jsem si udělala vždy vektory V-A, V-B a chtěla jsem si najít průsečík výšek a pak vypočítat jako vzdálenost dvou bodů. ale měla jsem tam moc neznámých, takže jsem si řekla, že je to asi špatný postup.

Děkuji za radu.

gadgetka · 12. 04. 2015 01:02

Není to vzdálenost těžiště trojúhelníkové podstavy od vrcholu D? ;)

byk7 · 12. 04. 2015 01:20

Řekl bych spíš, že se tím myslí vzdálenost bodu D od roviny ABC.

Potom je možné si vyjádřit objem čtyřstěnu dvěma způsoby, prvně ho dokážeme určit pomocí smíšeného součinu vektorů AB, AC, AD, a za druhé ho dokážeme určit pomocí obsahu trojúhelníka ABC a výšky v_d. Pak stačí tyto objemy porovnat.

Nebo je také možné určit rovnici roviny ABC a pro výpočet vzdálenosti bodu od roviny existuje nějaký vztah.

Freedy · 12. 04. 2015 02:02

↑ byk7:
nebo je také možné vytvořit obecný vzorec pro vzdálenost bodu D od roviny ABC, kde
$A=[a_1,a_2,a_3]$
$B=[b_1,b_2,b_3]$
$C=[c_1,c_2,c_3]$
$D=[d_1,d_2,d_3]$
A poté jednoduše dosadit konkrétní hodnoty do výsledného vzorce :)

EvBes · 12. 04. 2015 08:07

Děkuji, nenapadlo ě to udělat jako rovinu a bod. Děkuji za nápad, už vím :).

Matematické Fórum

#1 12. 04. 2015 00:28

Analytická geometrie - čtyřstěn

#2 12. 04. 2015 01:02

Re: Analytická geometrie - čtyřstěn

#3 12. 04. 2015 01:20

Re: Analytická geometrie - čtyřstěn

#4 12. 04. 2015 02:02

Re: Analytická geometrie - čtyřstěn

#5 12. 04. 2015 08:07

Re: Analytická geometrie - čtyřstěn

Zápatí