Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Variační počet - Koncový bod omezený rovností (TOTO TÉMA JE VYŘEŠENÉ)
#1 09. 04. 2015 13:43
- Aquabellla

- Moderátorka Bellla

- Místo: Brno
- Příspěvky: 1473
- Škola: Ma-Ek PřF MUNI (11-14, Bc.), (14-16, Mgr.)
- Pozice: Absolventka Bc., studentka NMgr.
- Reputace: 98
Variační počet - Koncový bod omezený rovností
Zdravím, mám další příklad z variačního počtu a nevím, jak ho dokončit. Asi se jedná jen o nějakou maličkost, ale můj mozek už to sám nezvládá :-)
Najdi křivky, pro které  může mít extrémy splňující
může mít extrémy splňující  , jestliže bod
, jestliže bod  musí ležet na přímce
musí ležet na přímce  .
.
Eulerova rovnice:  , kde
, kde 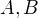 jsou konstanty.
jsou konstanty.
Počáteční bod: 
Koncový bod musí splňovat rovnici  v
v 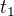 , kde
, kde 
 ,
,  ,
,  v
v 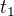 , kde
, kde  je konstanta.
je konstanta.
Jak postupovat dál?
Předem děkuji za každou radu.
Nejkratší matematický vtip: „Nechť epsilon je záporné…“
Zákon pro pedagogy: Nikdo vás neposlouchá, dokud se nespletete.
Offline
- (téma jako vyřešené označil(a) Aquabellla)
#2 09. 04. 2015 17:19
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: Variační počet - Koncový bod omezený rovností
Ahoj, co znamená tato věta:
Aquabellla napsal(a):
Najdi křivky, pro které
může mít extrémy splňující
? Moc nechápu smysl.
"Máte úhel beta." "No to nemám."
Offline
#3 10. 04. 2015 12:12 — Editoval Jj (10. 04. 2015 14:06) Příspěvek uživatele Jj byl skryt uživatelem Jj. Důvod: Zřejmě omyl
#4 10. 04. 2015 20:56 — Editoval Aquabellla (10. 04. 2015 20:57)
- Aquabellla

- Moderátorka Bellla

- Místo: Brno
- Příspěvky: 1473
- Škola: Ma-Ek PřF MUNI (11-14, Bc.), (14-16, Mgr.)
- Pozice: Absolventka Bc., studentka NMgr.
- Reputace: 98
Re: Variační počet - Koncový bod omezený rovností
↑ check_drummer:
To byl pokud o překlad do češtiny, asi ne moc zdařilý. Zde je originál:
Jednoduše řečeno: Je třeba najít extremálu k zadanému funkcionálu, která splňuje fixní počáteční bod  a omezený koncový bod, který musí ležet na přímce
a omezený koncový bod, který musí ležet na přímce  .
.
Nejkratší matematický vtip: „Nechť epsilon je záporné…“
Zákon pro pedagogy: Nikdo vás neposlouchá, dokud se nespletete.
Offline
#5 11. 04. 2015 11:23 — Editoval kafe_arabica (11. 04. 2015 11:28)
- kafe_arabica
- Příspěvky: 38
- Reputace: 3
Re: Variační počet - Koncový bod omezený rovností
Ahoj.
Čo je R za funkciu?
Prečo si podmienku pre koncový bod nevyužila nasledovne:
Koncový bod riešenia, teda tej krivky, musí ležať na priamke t-5. Koncový bod je 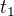 , t.j.
, t.j.  .
.
A už mám rovnice, 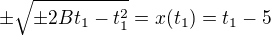 .
.
Môžeš, prosím, pripomenúť ako sa rieši tá diferenciálna rovnica?
Edit: Mimochodom, niekedy môže výjsť, už po dosadení počiatočných podmienok, krivka x, v ktorej je nejaká konštanta naviac. Napr.,  . Vtedy sa táto krivka dosadí do pôvodného integrálu, spočíta sa integrál a pozrie sa na extrém výslednej funkcie, príčom premenná bude samozrejme tá konštanta.
. Vtedy sa táto krivka dosadí do pôvodného integrálu, spočíta sa integrál a pozrie sa na extrém výslednej funkcie, príčom premenná bude samozrejme tá konštanta.
Offline
#6 11. 04. 2015 18:36
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: Variační počet - Koncový bod omezený rovností
↑ Aquabellla:
Ahoj, stále nechápu na jaké množině hledáme to maximum toho funkcionálu. Zaráží mě to spojení "can have" - to má asi naznačit, že hledáme nějakou nutnou podmínku existenci extrému (a nikoli nutně postačující)? Tedy úloha je taková, že mezi libovolnými křivkami splňujcíími x(0)=0 a (v bodě a)) x1=t1-5 chceme najít takovou maximalizující ten integrál - resp. takovou, iu které je podezření, že tento ntegrál maximalizuje...(?)
"Máte úhel beta." "No to nemám."
Offline
#7 12. 04. 2015 08:49
Re: Variační počet - Koncový bod omezený rovností
↑ Aquabellla: ↑ check_drummer:
Dobrý den.
Před pár dny jsem zkoušel úlohu dořešit, narazil jsem na problém - po dosazení mého řešení extrémály integrál divergoval. Takže možná, ...
Pokud se tedy nemýlím.
Offline
#8 12. 04. 2015 17:10
- Aquabellla

- Moderátorka Bellla

- Místo: Brno
- Příspěvky: 1473
- Škola: Ma-Ek PřF MUNI (11-14, Bc.), (14-16, Mgr.)
- Pozice: Absolventka Bc., studentka NMgr.
- Reputace: 98
Re: Variační počet - Koncový bod omezený rovností
↑ kafe_arabica: je funkce, která určuje omezení konečného bodu, tj.
je funkce, která určuje omezení konečného bodu, tj.  . V tomto příkladu to je
. V tomto příkladu to je  .
.
Jelikož v integrandu chybí proměnná  , tj.
, tj. 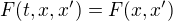 , Eulerova rovnice se dá zjednodušit na tvar:
, Eulerova rovnice se dá zjednodušit na tvar:  , což nám dá diferenciální rovnici 1. řádu, která se většinou spočte jednodušeji než DR 2. řádu, kterou dostaneme, použijeme-li základní tvar Eulerovy rovnice, tj.
, což nám dá diferenciální rovnici 1. řádu, která se většinou spočte jednodušeji než DR 2. řádu, kterou dostaneme, použijeme-li základní tvar Eulerovy rovnice, tj.  .
.
Děkuji moc za nápovědu k řešení, už jsem se dopočítala výsledku.
↑ check_drummer:
Ano, přesně tak. Jedná se o úlohu, která má procvičit omezení koncového bodu.
Pro zjištění, zda se skutečně jedná o optimum, je třeba vypočítat  . Při maximalizaci musí být
. Při maximalizaci musí být  a při minimalizaci
a při minimalizaci  pro
pro  , v tomto příkladu je
, v tomto příkladu je  .
.
↑ Jj:
Děkuji za upozornění, dám si na to pozor, až budu vybírat příklady do DP.
Nejkratší matematický vtip: „Nechť epsilon je záporné…“
Zákon pro pedagogy: Nikdo vás neposlouchá, dokud se nespletete.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Variační počet - Koncový bod omezený rovností (TOTO TÉMA JE VYŘEŠENÉ)
