Matematické Fórum

Zlatohlavok · 12. 04. 2015 11:11

Ahojte, mám tu jeden príklad s ktorým si vôbec neviem rady. Viete mi povedať ako by sa dal vypočítať?
Ďakujem pekne :-)

//forum.matweb.cz/upload3/img/2015-04/29858_Sn%25C3%25ADmka%2Bobrazovky%2B2015-04-12%2Bo%25C2%25A010.15.22.png

vanok · 12. 04. 2015 12:27

Ahoj ↑ Zlatohlavok:,
Podla textu cvicenia si v euklidovskom priestore ( inac by sme nemohli hovorit o uhloch). Cize staci vediet co urobi otocenie 180°.
Obraz vektorov standartnej bazy (1,0), (0,1) su vektory (-1,0),(0,-1).
Co ti hned da vhodnu maticu.....

Zlatohlavok · 12. 04. 2015 13:17

Ano správna odpoved je (-1,0),(0,-1), ale ako si k tomu prisiel? neviem asi mi unika pointa. :-)

Ako viem ,ze prave (-1,0),(0,-1) je otocenie o 180 stupnov?
Co keby tam bolo otocte o 90 stupnov?

Ďakujem

Al1 · 12. 04. 2015 13:37 — Editoval Al1 (12. 04. 2015 13:38)

↑ Zlatohlavok:

Zakresli si oba vektory v soustavě souřadnic, umísti si je oba do počátku. A teď je otoč ve směru chodu hodinových ručiček o 180 st. Vektor (1;0) se otočí do vektoru opačného (-1;0) a totéž platí pro druhý vektor. Rotace o 180st. je vlastně středová souměrnost, která má stejný střed jako rotace.

Na druhou otázku si již odpovíš sám - rotace 90 st.

vanok · 12. 04. 2015 14:05

↑ Zlatohlavok:,
Tvoja otazka je vlastne vediet ze nejaka linearna aplikacia je urcena obrazom vektorov ( lubovolnej) baze.
To preto, lebo v danej baze, kazdy vektor sa da vyjadrit ako LK vektorov tej bazy.( Preto hovorime o suradnicach) a ked si uvedomis ako je definovana linearna aplikacia, tak je to jasne.
Staci?

Zlatohlavok · 12. 04. 2015 16:03

Nevim ,celkom tomu nerozumiem. Neviem či je to tak vždy, ale asi áno. Našiel som si , že vychádzame z (1,0)(0,1)
Potom som sa to naucil, ako sa otáča postupne po 90 stupňov.
Nerozumiem princípu, ale naučil som sa to.

o 90
(0,-1),(1,0)

o 180
(-1,0)(0,-1)

o 270

(0,1)(-1,0)

vanok · 12. 04. 2015 16:28

↑ Zlatohlavok:,
Takychto cviceniach sa vzdy otaca okolo pociatku ( ak by to bolo inac by to bolo povedane)
Metoda ( lopatisticka) nakresli dva krat vektory bazy tak ze vychadzaju z pociatku O. Potom pichni nejaky spendlik cez dva papiere cez pociatok a potoc vrchny papier o dany uhol a urci aka je poloha danych potocenych vektoroch na papiery co sa nepohol.

Zlatohlavok · 12. 04. 2015 19:00

Práve si pozerám ďalší podobný príklad a tu je práve otočenie o 90 stupňov a výsledok je (0,1)(-1,0)

Ale podla všetkého čo som sa naučil a je totak aj na wiky, by to malo byť (0,-1)(1,0).

//forum.matweb.cz/upload3/img/2015-04/58017_Sn%25C3%25ADmka%2Bobrazovky%2B2015-04-12%2Bo%25C2%25A018.57.10.png

vanok · 12. 04. 2015 19:17

Otocenie vektoru (1,0) o 90° vo smere ako hodinky da (0,-1)
(0,1). (1,0)
To da druhu maticu.

Zlatohlavok · 14. 04. 2015 11:14

Píšeš, že:
Otocenie vektoru (1,0) o 90° vo smere ako hodinky da (0,-1)
(0,1). (1,0)
To da druhu maticu.

Ale ved druha matica je ( 0 1 )
(-1 0 )

nie toto ako píšeš
(0,-1)
(1,0)

Dakujem za objasnenie, uz som myslel, ze tomu chapem, ale zas som mimo. ked to otocim o 90 stupnov, tak dostanem (0,-1)
(1,0)
ale spravna odpoved je ( 0 1 )
(-1 0 )

vanok · 14. 04. 2015 12:05

↑ Zlatohlavok:,
Ano, lebo musis pozerat na stlpce.
Overis To tak, ze druhu maticu vynasobis, stlpcom
1
0

A potom stlpcom
0
1
V nasobeni matrice vektory su vyjadrene stlpcamy,

Rumburak

↑ Zlatohlavok:

Ahoj. Zdravím také kolegu ↑ vanok:.

Vektor $(x, y)$ můžeme zapsat ve tvaru komplexního čísla $z = x + y \mathrm{i}$ .
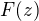Nechť $F(z)$ je vektor (rovněž zapsaný ve tvaru komplexního čísla), který získáme otočením vektoru $z$
o úhel $\varphi$ okolo počátku soustavy souřadnic.

Z věty o součinu komplexních čísel v goniometrickém tvaru plyne vztah

$F(z) = (\cos \varphi + \mathrm{i} \sin \varphi) z$ .

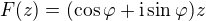Když tuto rovnost přepíšeme pomocí součinu matice s vektorem v jebo "klasickém" tvaru $(x, y)$ , snadno
obdržíme výsledek.

Zlatohlavok · 14. 04. 2015 14:33

Rumburak, tak tam teda doplnim cisla.

Majme teda yaciatok
1 0
0 1

Co je x, y? Idem po riadkoch? Teda najskor je x=1, y=0?
z=1+0i = 1

F(z)=(cos90 + i*sin90) * z
F(z)=(0 + i*1) * 1 = i

Takto?

Dakujem

vanok · 14. 04. 2015 14:43 — Editoval vanok (14. 04. 2015 14:53)

Pozdravujem ↑ Rumburak:,
Pochopitelne komplexna reprezentacia je mocny a dobry nastroj.
No ale aj kolega ↑ Zlatohlavok: to videl v skole maticou metodou tak ju tiez musi ovladat cf. ↑ vanok:.
Idem vyeditovat ako doplnok, este nieco na Wikipedii, za chvilku to sem pridam.
Edit
http://en.m.wikipedia.org/wiki/Transformation_matrix

Tu su dobre informacie na tvoju temu. A sa mozes viac dozvediet ako v specialnom pripade $R^2$ .
Najviac tam najdes aj matice otoceni o vseobecny uhol.
A tu mas nieco v dim.2
http://www.miniphysics.com/coordinate-t … ation.html
Aj mas este otazky, nevahaj a napis.

Rumburak

↑ Zlatohlavok: , ↑ vanok:

Otázkou je, zda a jak byl ten "maticový" vzorec ve škole odvozen. U vzorců, kterým nerozumíme,
protože neznáme jejich zdůvodnění, je těžké si je pamatovat a mít jistotu při jejich používání
(moje zkušenost).

Já bych doporučoval začít tím odvozením (pro obecný případ, samozřejmě). Ale nic nevnucuji :-).

Autor skryl část textu. Zobrazit/skrýt!

Zlatohlavok · 14. 04. 2015 15:31

Práve som zistil, ze mne staci vediet:
cos fi sin fi
-sin fi cos fi

Tu si dosadim uhol a mam.

Toto som presne potreboval vediet.

Pochopil som to spravne?

Rumburak · 14. 04. 2015 15:42

↑ Zlatohlavok:

Ano, pokud zobrazení má mít tvar F(z) = z*M , kde vektory z, F(z) jsou zapsány "řádkově".

vanok · 14. 04. 2015 16:34

Poznamka
V prvom prispevku pises, ze tvoja matica aplikacie je napisana tak ze nasobi zlava ↑ Zlatohlavok:. Co to znamena?

Zlatohlavok · 14. 04. 2015 20:43

Neviem co to znamena, to som sem dal len screen zadania.

vanok · 14. 04. 2015 21:08

↑ Zlatohlavok:,
To znamena ze matica sa napise v lavo.
Ax
A je matica, x je stlpcovy vektor.

Matematické Fórum

#1 12. 04. 2015 11:11

Zobrazenie a matica

#2 12. 04. 2015 12:27

Re: Zobrazenie a matica

#3 12. 04. 2015 13:17

Re: Zobrazenie a matica

#4 12. 04. 2015 13:37 — Editoval Al1 (12. 04. 2015 13:38)

Re: Zobrazenie a matica

#5 12. 04. 2015 14:05

Re: Zobrazenie a matica

#6 12. 04. 2015 16:03

Re: Zobrazenie a matica

#7 12. 04. 2015 16:28

Re: Zobrazenie a matica

#8 12. 04. 2015 19:00

Re: Zobrazenie a matica

#9 12. 04. 2015 19:17

Re: Zobrazenie a matica

#10 12. 04. 2015 20:51 Příspěvek uživatele Zlatohlavok byl skryt uživatelem Zlatohlavok. Důvod: nie , nechapem tomu stale

#11 14. 04. 2015 11:14

Re: Zobrazenie a matica

#12 14. 04. 2015 12:05

Re: Zobrazenie a matica

#13 14. 04. 2015 13:46 — Editoval Rumburak (14. 04. 2015 14:27)

Re: Zobrazenie a matica

#14 14. 04. 2015 14:33

Re: Zobrazenie a matica

#15 14. 04. 2015 14:43 — Editoval vanok (14. 04. 2015 14:53)

Re: Zobrazenie a matica

#16 14. 04. 2015 15:28 — Editoval Rumburak (14. 04. 2015 15:32)

Re: Zobrazenie a matica

#17 14. 04. 2015 15:31

Re: Zobrazenie a matica

#18 14. 04. 2015 15:42

Re: Zobrazenie a matica

#19 14. 04. 2015 16:34

Re: Zobrazenie a matica

#20 14. 04. 2015 20:43

Re: Zobrazenie a matica

#21 14. 04. 2015 21:08

Re: Zobrazenie a matica

Zápatí