Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 15. 04. 2015 10:33
- Crashatorr
- Příspěvky: 360
- Reputace: 7
Důkaz podgrupy
Zdravím, vůbec si nevím rady s tímto úkolem, mohl by prosím někdo pomoci?
Nechť X je neprázdná podmnožina grupy (G,  ) a nechť
) a nechť 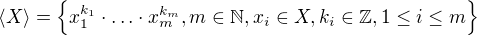
Ukažte že  pro ka6dou podgrupu H grupy (G,
pro ka6dou podgrupu H grupy (G,  ) splňující podmínku
) splňující podmínku 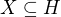
Offline
- (téma jako vyřešené označil(a) Crashatorr)
#2 15. 04. 2015 14:17
Re: Důkaz podgrupy
↑ Crashatorr:
Ahoj. Je to velmi jednoduché.
Předpokládejme, že 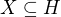 , kde
, kde  je grupa (ať již podgrupa grupy
je grupa (ať již podgrupa grupy  čí jiná) a
čí jiná) a
 .
.
Především pro všechna uvažovaná  je
je 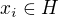 , jak plyne z předpokladu
, jak plyne z předpokladu 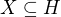 .
.
Dále se využije
- skutečnost, že grupa (v našem případě grupa  ) je uzavřená na součin a na operaci inversního prvku,
) je uzavřená na součin a na operaci inversního prvku,
- definice mocniny,
a ke slovu příjde také indukce (dokonce dvakrát, pokud důkaz má být hodně elementární).
Offline