Matematické Fórum

smajdalf · 13. 04. 2015 11:46

Ahoj všem,
pomohl by mi někdo s tímhle příkladem:

14. Je dán trojúhelník ABC s obsahem S a body K, L a M po řadě uvnitř stran AB, BC a CA tak, že platí |AK| : |KB| = |BL| : |LC|= |CM| : |MA| = 1 : 2. Vyjádřete obsahy všech částí, na něž je trojúhelník ABC rozdělen úsečkami AL, BM a CK.

Ještě jsem si označil průsečíky 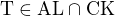$\text{T} \in \text{AL} \cap \text{CK}$ , $\text{U} \in \text{AL} \cap \text{BM}$ , $\text{V} \in \text{BM} \cap \text{CK}$

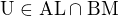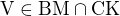
Začátek bych měl asi takto: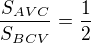
$\frac {S_{AVC}}{S_{BCV}} = \frac{1}{2}$
$\frac {S_{AKV}}{S_{KBV}} = \frac{|AK|}{|KB|} = \frac{1}{2} = \frac{S_{AKC}}{S_{KBC}}$

A ještě mám v sešitě poznámku, že: 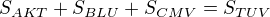$S_{AKT}+S_{BLU}+S_{CMV} = S_{TUV}$

Ale jak dál?

Akojeto · 13. 04. 2015 13:17

↑ smajdalf:

No - neviem.

//forum.matweb.cz/upload3/img/2015-04/23774_image.jpg

jelena · 13. 04. 2015 21:53 — Editoval jelena (14. 04. 2015 20:23)

Zdravím,

↑ smajdalf: pokud by to nemělo být prostředky ZŠ, tak lze v tom hodně používat poměry obsahů trojúhelníků ve tvaru vzorce 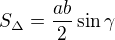$S_{\Delta}=\frac{ab}{2}\sin \gamma$ (poměr obsahů původního trojúhelníku k "menšímu" se stejným úhlem mezi stranami a využitím poměru délky původního trojúhelníku a "zmenšené" strany. Tak jsi zkoušel? Děkuji.

Edit: užití předchozího doporučení je dobré provádět postupně - nakreslit jednu dělicí přímku, doplnit obsahy vzniklých útvarů a až poté zakreslit další přímku.

Edit 2: po předchozím editu mi došlo, že nemusím používat vzorec se sin, mohu i s výškou na stranu, jelikož po dělení vždy pracuji s původní výškou, jen se úměrně mění strana (tedy ZŠ).

vanok · 14. 04. 2015 15:26

Ahoj ↑ smajdalf:,
V tvojich prispevkoch nam davas ocislovane cvicenia typu priprava na olympiady.
Mozes nam upresnit ich povod. Dakujem

jelena · 14. 04. 2015 20:24

↑ vanok:

Zdravím, s kolegou v některém z jeho témat jsme diskutovali, že sbírka je tato - pro přípravu budoucích učitelů k vedení přípravy vlastních studentů (žáku) k olympiádě. Je to výběr soutěžních úloh, tedy v různých obměnách se dají najít ve speciálních sbírkách vč. principů řešení, v archivech olympiád a dalších soutěží.

Tedy pro kolegu ↑ smajdalf: předpokládám přínosnější metodu jako takovou (než řešení) i včetně teorie okolo, pro další čtenáře sekce snad může prospět v přípravách.

vanok · 14. 04. 2015 21:48 — Editoval vanok (14. 04. 2015 21:49)

Pozdravujem ↑ jelena:,
Dakujem za tu zbierku. Na prvy pohlad ide o zaujimavu zbierku pre buducich vyucujucich.
Mozno by bolo zaujimaveurobit novu sekciu: uzitocne cvicenia pre ( buducich ) vyucujucich. Co by doplnilo didakticku sekciu.

Co sa tyka daneho cvicenia.
Jeden iny ( zaujimavy) pristup je najprv popisat ako sa dostaneme od maleho trojuholnika UVT kutrojuholniku ABC
Potom v niecom sa dane cvicenie lahsie vyriesi.
Iny mozny postup je vyuzitie afinity ( ako je to dovolene): potom staci napr. vyriesit cvicenie pre rovnostranny trojuholnik.
Dalsia metoda= analyticka geometria.
( No pozor, nie vsetki metody funguju pre zakladoskolakov)

jelena · 15. 04. 2015 20:15

↑ vanok:

Také pozdrav,

zatím bych řekla, že při uváženém (s vhodným úvodem) umístění dotazů budoucích učitelů se dá vystačit ve stávajících sekcích (pokud chtějí, aby na dotaz odpovídal žák určitého stupně, nebo potřebuji doporučení k dotazu) + sekce didaktiky - pokud je téma více metodické, než "k řešení". Materiálů je teď porůznu dost jak online, tak v knižní formě.

Co sa tyka daneho cvicenia.

autor sbírky dává odkaz na konkrétní diplomovou práci + uvádí, že na cvičení probere obecné postupy. Tak uvidíme, jak s tím vším, co jsi doporučil + školní materiály kolega naloží, snad téma ještě doplní.

Matematické Fórum

#1 13. 04. 2015 11:46

Trojúhelník a poměr stran - obsah jeho částí

#2 13. 04. 2015 13:17

Re: Trojúhelník a poměr stran - obsah jeho částí

#3 13. 04. 2015 21:53 — Editoval jelena (14. 04. 2015 20:23)

Re: Trojúhelník a poměr stran - obsah jeho částí

#4 14. 04. 2015 15:26

Re: Trojúhelník a poměr stran - obsah jeho částí

#5 14. 04. 2015 20:24

Re: Trojúhelník a poměr stran - obsah jeho částí

#6 14. 04. 2015 21:48 — Editoval vanok (14. 04. 2015 21:49)

Re: Trojúhelník a poměr stran - obsah jeho částí

#7 15. 04. 2015 20:15

Re: Trojúhelník a poměr stran - obsah jeho částí

Zápatí