Matematické Fórum

matge · 18. 04. 2015 13:06

Mám dotaz - mám příklad

$\sum_{n=1}^{\infty }\frac{(-1)^n}{\sqrt{(n+1)(n+2)(n+3)(n+4)}}$

Vyjde mi
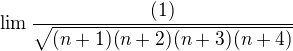$\lim\frac{(1)}{\sqrt{(n+1)(n+2)(n+3)(n+4)}}$ se rovná nule

když porovnám
$\frac{(1)}{\sqrt{(n+1+1)(n+2+1)(n+3+1)(n+4+1)}} <\frac{(1)}{\sqrt{(n+1)(n+2)(n+3)(n+4)}}$ tak to mi taky platí a z toho vím, že řada je konvergentní

Jak ale určím, je-li konvergentní absolutně nebo relativně?
když jsem si dal podílové a odmocninové kritérium, vyšlo mi 1, čímž to nerozhodnu, na integrálové je to moc složité, ale zbývá mi tedy pouze srovnávací kritérium, to ale nevím, s jakou řadou mám srovnávat.

Jaký bude tedy výsledek ohledně absolutní/relativní kovergenci? (pokud možno, prosím i o postup)
Děkuji

Eratosthenes · 18. 04. 2015 14:23

ahoj ↑ matge:

Použil bych spíš srovnávací kriterium:

$\frac 1 {\sqrt{(n+1)(n+2)(n+3)(n+4)}} < \frac 1 {\sqrt{n\cdot n \cdot n \cdot n}}=\frac 1 {n^2}$

matge · 18. 04. 2015 15:35 — Editoval matge (18. 04. 2015 15:36)

↑ Eratosthenes:
Ahoj,
takže udělal jsem to takto:
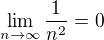- srovnácím kritériem mi vyjde, že $\sum_{n=1}^{\infty }\frac{1}{n^2}$ vypočtu přes limitu $\lim_{n\to\infty }\frac{1}{n^2} =0$ a podle toho, když mi konverguje tato řada, tak mi konverguje i má původní $\sum_{n=1}^{\infty }\frac{(-1)^n}{\sqrt{(n+1)(n+2)(n+3)(n+4)}}$ no a protože přes Leibnitze (viz můj příspěvek výše) mi vyšla $lim=0$ a $a_{n+1}<a_{n}$ , tak je tato řada $\sum_{n=1}^{\infty }\frac{(-1)^n}{\sqrt{(n+1)(n+2)(n+3)(n+4)}}$ absolutně kovergentní, je to tak?

Eratosthenes · 18. 04. 2015 15:48

Ahoj ↑ matge:,

Není to tak. Podmínka lim a_n = 0 je pro konvergenci nutná, nikoli však postačující. K ověření konvergence řady $\sum_{n=1}^{\infty }\frac{1}{n^2}$ použij d'Alambertovo kriterium.

matge · 18. 04. 2015 15:57 — Editoval matge (18. 04. 2015 16:12)

ahoj ↑ Eratosthenes:
ale když použiju limitní d'Alambertovo kritérium (podílové) $lim|\frac{\frac{1}{(n+1)^2}}{\frac{1}{n^2}}|$ tak mi limita vyjde 1 a to přece nerozhodnu o absolutní/relativní konvergenci...

když ale ten výraz rozhodnu podle integrálního kritéria, vyjde mi nekonečno. Tudíž znamená to pak, že ta zadaná řada je relativně konvergentní?

Pokud nemám pravdu, chtěl bych tě prosím, poprosit o "vzorové" řešení, jak mám rozhodnout o absolutní konvergenci/ relativní konvergenci/ divergenci.

vanok · 18. 04. 2015 16:24 — Editoval vanok (18. 04. 2015 16:27)

Pozdravujem,
Najprv matematici si zasluzia zasluzia aby sa ich mena pisali neskomolene.
Lebo potom, ako rozumiet kriteria neexistujucich matematikov z cudnimi menami, ako vyssie v tomto vlakne?

Autor skryl část textu. Zobrazit/skrýt!

Inac v tomto cviceni sa da pouzit aj http://en.m.wikipedia.org/wiki/Alternating_series_test
ktore sa ici uz v prvom rocniku vysokych skol.

Eratosthenes

ahoj ↑ matge:,

d'Alembertovo kriterium opravdu nepomůže (to jsem nějak nedomyslel), ale integrální určitě ano - nekonečno tam asi nevyjde:

$\int_1^\infty \frac 1 {x^2} dx= \lim_{t\to\infty} \int_1^t \frac 1 {x^2} dx = \lim_{t\to\infty}\left[ -\frac 1 x\right]_1^t =...$

matge · 18. 04. 2015 16:34

ahoj↑ Eratosthenes:
jo, máš pravdu, blbě jsem se podíval :)
takže výsledkem tedy je integrálového je 1, tudíž z toho se dá odvodit, že tedy ta původní řada tedy je absolutně konvergentní?

Eratosthenes

Zdravím ↑ vanok:

Jako motto máš "MOJ PRINCIP ... UKAZAT AKO SA K ODPOVEDI DOSTAT". Obávám se, že jízlivým poukazováním na překlepy toto krédo nenaplníš. Jestliže opravdu neznáš kriterium, o které tady jde, pak opravdu nevím, co bych na to řekl.

Odkaz, který doporučuješ, řeší konvergenci - ale o ni tady přece nejde. Tady se s kolegou ↑ matge: snažíme vyřešit to, zda jde o konvergenci absolutní, anebo relativní.

PS: Nevím, jak kde, ale já znám spoustu škol, kde se tyto otázky řeší až ve druhém ročníku...

Eratosthenes · 18. 04. 2015 16:49

ahoj ↑ matge:,

OK.

vanok · 18. 04. 2015 16:59 — Editoval vanok (18. 04. 2015 17:27)

Mily ↑ Eratosthenes: ,
Prestan si robit svandu. Pisem, ze to meno tu bolo viac krat spatne napisane a ze matematici si zasluzia respekt.
A to je skoda.
Ze niektore veci sa ucite na tvojej skole neskor ako inde, to nie je podstatne.
Inac ja ti pisem slusne a respektujem tvoju ossobu. To by si sa mohol aj ty naucit.

A potom na konvergenciu rady, $\frac 1{n^2}$ mas k disposicii aj jednoduchsiu metodu ak vies, ze $\frac 1{n^2}\le \frac 1 { n-1} - \frac 1 n$ .

Autor skryl část textu. Zobrazit/skrýt!

matge · 18. 04. 2015 17:01

ahoj ↑ Eratosthenes:
Tak to jsem rád, že jsem se díky tobě dokopal k výsledku. Takže dá se to shrnout takto (ne vždy teda to platí), ale že když použiju kritérium srovnávací, tak pak všechny ty ostatní aplikuji na tu řadu, kterou porovnávám a ne na tu původní? A když mi to platí na tu řadu, se kterou to porovnávám, tak to často platí i na tu původní?
Dík

Eratosthenes · 18. 04. 2015 19:57

ahoj ↑ matge:,

postup zjišťování konvergence řady

$\sum (-1)^n a_n;a_n>0$

je obecně takový:

a) Je-li 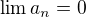$\lim a_n = 0$ , řada konverguje, jinak ne.

b) Konvergence z bodu a) může být relativní nebo absolutní. Řada

$\sum (-1)^n a_n;a_n>0$

konverguje absolutně právě tehdy, když konverguje řada

$\sum a_n$

K absolutní konvergenci už podmínka 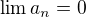$\lim a_n = 0$ nestačí a je potřeba použít dalších kriterií. Např. srovnávacího tak, jak jsme to udělali my -

najdu majorantu, tj. řadu, kde od jistého indexu platí $a_n\le b_n$ a dokážu konvergenci $\sum b_n$ (např. integrálním kriteriem tak, jak jsme to udělali my).

vanok · 18. 04. 2015 22:16

Mily ↑ Eratosthenes:,
Ako vidim, pochopil si moju poznamku ↑ vanok:. Tak vidis ze bola uzitocna.
Rad som ti pomohol.
Dobre pokracovanie.

Matematické Fórum

#1 18. 04. 2015 13:06

řada - konvergence, divergence

#2 18. 04. 2015 14:23

Re: řada - konvergence, divergence

#3 18. 04. 2015 15:35 — Editoval matge (18. 04. 2015 15:36)

Re: řada - konvergence, divergence

#4 18. 04. 2015 15:48

Re: řada - konvergence, divergence

#5 18. 04. 2015 15:57 — Editoval matge (18. 04. 2015 16:12)

Re: řada - konvergence, divergence

#6 18. 04. 2015 16:24 — Editoval vanok (18. 04. 2015 16:27)

Re: řada - konvergence, divergence

#7 18. 04. 2015 16:28 — Editoval Eratosthenes (18. 04. 2015 16:31)

Re: řada - konvergence, divergence

#8 18. 04. 2015 16:34

Re: řada - konvergence, divergence

#9 18. 04. 2015 16:49 — Editoval Eratosthenes (18. 04. 2015 16:51)

Re: řada - konvergence, divergence

#10 18. 04. 2015 16:49

Re: řada - konvergence, divergence

#11 18. 04. 2015 16:59 — Editoval vanok (18. 04. 2015 17:27)

Re: řada - konvergence, divergence

#12 18. 04. 2015 17:01

Re: řada - konvergence, divergence

#13 18. 04. 2015 19:57

Re: řada - konvergence, divergence

#14 18. 04. 2015 22:16

Re: řada - konvergence, divergence

Zápatí