Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 19. 03. 2015 18:30 — Editoval Tomas5 (19. 03. 2015 18:39)
rovnice symetrie podle roviny
Dobrý den,
určete rovnice symetrie podle roviny 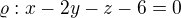 .
.
Postupoval jsem podle vzorového příkladu ve skriptech Ježek: Geometrie 2 pro FST tak, že jsem určil normálový vektor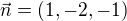 a zvolil jsem bod X na rovině pro
a zvolil jsem bod X na rovině pro  a
a  tedy
tedy ![kopírovat do textarea $X=[6,0,0]$](/mathtex/ca/cafb72141fda84f21cea18e0d106e6fe.gif) . Normálový vektor roviny xy je
. Normálový vektor roviny xy je 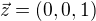 . Úhel otočení je
. Úhel otočení je  ,
,  ,
, 
Dosadím d vzorce 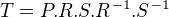






Vynásobím postupně tyto matice a vychází mi špatný výsledek :
Nepožaduju řešení, jenom bych chtěl poprosit o radu jak mají být sestaveny ty matice P, R, S, R^{-1}, S^{-1} nebo kde mám chybu v jejich sestavení.
Děkuji za pomoc.
Offline
#2 20. 03. 2015 10:31 — Editoval Rumburak (20. 03. 2015 14:04)
Re: rovnice symetrie podle roviny
↑ Tomas5:
Ahoj.
Řekl bych, že metoda ze skript může svojí zbytečnou krkolomností i odrazovat od matematiky.
Hledáme prostorové zobrazení  takové, aby
takové, aby
1) vektor  pro každé
pro každé  byl
byl  - násobkem normálového vektoru dané roviny,
- násobkem normálového vektoru dané roviny,
kde reálné číslo  ovšem BUDE záviset na
ovšem BUDE záviset na  ;
;
2) bod  (v podstatě střed úsečky s krajními body
(v podstatě střed úsečky s krajními body  ) ležel v dané rovině.
) ležel v dané rovině.
Takže stačí sestavit potřebné rovnice a vypočítat z nich neznámou  . Vyjádřit pak zobrazení
. Vyjádřit pak zobrazení 
v požadovaném tvaru, v němž by figurovala matice této transformace, by už také nemělo být těžké.
Myslím, že skripta pro techniky ne vždy jsou vhodným studijním materiálem pro studenta MFF.
Offline
#4 20. 03. 2015 14:02 — Editoval Rumburak (20. 03. 2015 14:10)
Re: rovnice symetrie podle roviny
Máme rovinu 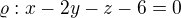 , jejímž normálovým vektorem je
, jejímž normálovým vektorem je  .
.
Připomeňme, že výraz 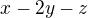 je skalárním součinem vektorů
je skalárním součinem vektorů 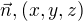 .
.
Nechť ![kopírovat do textarea $X = [x, y, z]$](/mathtex/96/964117be9e5b18ac3bd24ab0bbbe0d05.gif) je obecný bod prostoru,
je obecný bod prostoru, ![kopírovat do textarea $P = [0, 0, 0]$](/mathtex/e4/e47b14f6858554756051af0b5c147c5d.gif) počátek soustavy souřadnic.
počátek soustavy souřadnic.
Rovnici roviny  , pak můžeme pomocí skalárního součinu vektorů psát v přehlednějším tvaru
, pak můžeme pomocí skalárního součinu vektorů psát v přehlednějším tvaru
(0)  .
.
Je-li 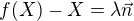 , potom
, potom  a
a
(1) 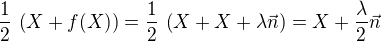 .
.
Tento bod má patřit do roviny  , tedy musí být dle (0) splněna rovnice
, tedy musí být dle (0) splněna rovnice
 ,
,
odtud snadno  ,
,  .
.
Napsal jsem, že "reálné číslo  nebude záviset na
nebude záviset na  ", ale to byl, jak je vidět, můj omyl, za který se
", ale to byl, jak je vidět, můj omyl, za který se
omlouvám.
Offline
#5 20. 03. 2015 14:21 — Editoval vanok (20. 03. 2015 14:24)
Re: rovnice symetrie podle roviny
Pozdravy,
Poznamka:
Dve metody v skratke
1)zmena reperu Bod M je v rovine
i,j dva ortogonalne vektory roviny
n normalny vektor na rovinu
V repery (M; n,i,j) mame s(n)=-n, s(i)=i, s(j)=j
To da maticu...a potom sa rate do povodneho reperu.
2)pouzitie znamej relacie 
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 20. 03. 2015 16:02
Re: rovnice symetrie podle roviny
Děkuji moc,
dostanu rovnici 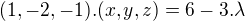 a vyjádřím
a vyjádřím  . X-ová souřdnice mi vyšla správně
. X-ová souřdnice mi vyšla správně 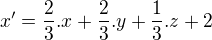 ale y-ovou a z-ovou souřadnici mám špatně podle výsledků. Nevím jestli se lambda mění nebo zůstává konstantní. Děkuji za radu.
ale y-ovou a z-ovou souřadnici mám špatně podle výsledků. Nevím jestli se lambda mění nebo zůstává konstantní. Děkuji za radu.
Offline
#9 21. 03. 2015 13:12
Re: rovnice symetrie podle roviny
Pozdravujem ↑ Rumburak:,
Pridavam pre uplnost jedno z rieseni o ktorych som vyssie pisal, co doplni tvoj pristup.
(pracujem poochopitalne v standardnej bazy)
Mame danu afinnu rovinu 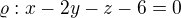 , ku ktorej jej asociovana jej vektorova rovina
, ku ktorej jej asociovana jej vektorova rovina .
.
Ich normalovy vector je
 .
.
Co nam da 
Akoze linearna cast hladanej symetrie  je
je 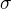 , ktora je pochopitelne ortogonalnana symetria vzladom k rovine
, ktora je pochopitelne ortogonalnana symetria vzladom k rovine  .
.
Bod  je v rovine
je v rovine  a preto
a preto  .
.
Pre lubovolny bod  mame
mame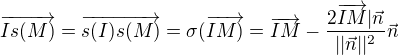
Akoze
 ,
,
dostaneme 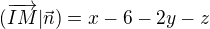 .
.
Tak mame 
Konecne dostaneme

Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#10 17. 04. 2015 14:37 — Editoval Rumburak (17. 04. 2015 15:22)
Re: rovnice symetrie podle roviny
↑ vanok:
Ahoj.
Děkuji za doplnění. Musel jsem si na prostudování najít čas - rozhodně nejde o příspěvek, který bych považoval
za snadno přístupný, což je do značné míry dáno mými mezerami ve znalostech geometrických metod. Proto
reaguji se zpožděním. Metoda je zajímavá, sám bych na ni určitě nepřišel .
Offline
#11 17. 04. 2015 15:23
- Eratosthenes
- Příspěvky: 2584
- Reputace: 132
Re: rovnice symetrie podle roviny
ahoj ↑ Tomas5:
měl jsi to asi celé dobře jen jsi špatně opsal vzoreček - musíš posunout (P), potom otočit (R) ozrcadlit (S) a potom zpátky otočit (R^{-1}) a pak ne ozrcadlit, ale posunout, takže ne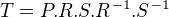
ale 
↑ Rumburak: : Mám zcela opačné zkušenosti. Tato metoda není krkolomná a už vůbec neodrazuje od matematiky - naopak. Když se pochopí, je velmi jednoduchá a navíc ukazuje zcela jednotný a univerzální postup, jak takové transformace programovat v grafických systémech.
PS: Říká se, že všechno, co člověk umí, je pro něj jednoduché. Nepochopitelné a složité je pro něj jenom to, co neumí.
Budoucnost patří aluminiu.
Online
#12 17. 04. 2015 15:50 — Editoval Rumburak (17. 04. 2015 15:57)
Re: rovnice symetrie podle roviny
↑ Eratosthenes:
Na tom úsloví je mnoho pravdy a na moji osobu a tento případ jistě sedí. Ale myslím si, že i kdybych ony metody ovládal,
v případě této úlohy bych je nepoužil - prostě proto, že řešit jednoduchou úlohu takovým způsobem (podle mého názoru
zbytečně složitým) by mi nepřišlo níjak zvlášť zajímavé. Je to samozřejmě věc mého osobního vkusu. Naštěstí nejsem
student a mohu si vybírat, kterou úlohu budu řešit a jak. Pokud se moje řešení bude hodit někomu dalšímu, tím lépe. :-)
Offline
#13 17. 04. 2015 16:11
- Eratosthenes
- Příspěvky: 2584
- Reputace: 132
Re: rovnice symetrie podle roviny
↑ Rumburak:
Každý samozřejmě ať si zvolí metodu, která mu vyhovuje. My takto se studenty skládáme zobrazení zcela běžně - hned v 1. ročníku asi ve druhém týdnu. Je to pro ně bezvadná příležitost procvičit násobení matic, které se právě naučili, i první setkání s izomorfismem, na kterém je vidět, že k něčemu je. Při ručním počítání samozřejmě skládáme do cca tří matic, u složitějších zobrazení (jako je toto) si stačí uvědomit, jak zrcadlo ztotožnit s některou souřadnicovou rovinou a jak ji potom vrátit zpátky. Násobení pak provede počítač.
Na téma komplikovanosti a odrazování od matematiky jsem kdesi viděl zajímavý příspěvek a možná v Ostaním založím na toto téma vlákno...
Budoucnost patří aluminiu.
Online
#14 17. 04. 2015 16:43
Re: rovnice symetrie podle roviny
↑ Eratosthenes:
Kursem lineární algebry jsem v prvním semestru také prošel, ale na geometrické souvislosti tam nebyl kladen velký důraz -
mohu-li to po těch letech posoudit. Navíc jsem patřil k těm studentům, kterým lépe šla analýza než algebra, zatímco u většiny
mých tehdejších spolužáků v ročníku tomu bylo právě naopak. Možná že i to se promítá do mého "vkusu" , mohu-li to
takto nazvat.
Do toho zamýšleného vlákna se určitě rád podívám.
Offline
#15 20. 04. 2015 11:19 — Editoval Rumburak (20. 04. 2015 15:23)
Re: rovnice symetrie podle roviny
↑ Eratosthenes:
Abychom si lépe rozuměli, ještě dodám:
I když s metodou doporučovanou v oněch skriptech nemám osobní zkušenost, její princip mi, domnívám se, není nejasný:
Hledaná isometrická tranformace se má nalézt tak, že se zkomponuje z jakýchsi transformací elementárních, jimiž jsou
například
- posunutí,
- symetrie podle souřadnicových (či jiných významných) rovin,
- otočení okolo souřadnicových os (či jiných významných přímek).
Transformační rovnice pro posunutí a pro symetrie dle souřadnicových rovin jsou zřejmé, rovnice pro otočení okolo těch os
už nikoliv, ale dají se s trochou trpělivosti odvodit (například pomocí znalostí o součinu komplexních čísel).
Avšak správně poskládat tyto elementární transformace tak, abychom dostali transformaci, kterou hledáme, klade, zdá se mi,
celkem vysoké nároky na prostorovou představivost a je proto snadné zde udělat chybu.
Trénovat prostorovou představivost je jistě důležitou průpravou strojaře, stavaře a neuškodí ani matematikovi. Avšak od
matematika (a kolega ↑ Tomas5: se k MFF hlásí) se zároveň očekává, že bude umět nalézt jednoduché řešení, pokud takové
existuje. A metoda založená na klasické analytické geometrii a spočívající v tom, že požadavky kladené na hledanou transformaci
zformulujeme pomocí dvou zřejmých rovnic, z nichž celkem snadno vypočteme neznámou reálnou funkcí  , na níž jedině řešení
, na níž jedině řešení
závisí, mi přece jen připadá poněkud jednodušší (i proto, že se nemusíme zabývat nezáživným násobením matic).
Snad jsem se mohl sdržet poněkud hanlivého hodnocení první metody - za tento svůj úlet se samozřejmě omlouvám.
Offline

 a
a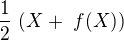 =
= 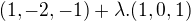
 a pro
a pro  je
je ![kopírovat do textarea $X = [0,-4,-4]$](/mathtex/42/4239cae7fec961453430cb787fec3691.gif) mám to asi špatně.
mám to asi špatně.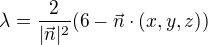
![kopírovat do textarea $f(x, y, z) = f(X) = X + \lambda \vec{n} = [x, y, z] + \frac{2}{ |\vec{n}|^2}(6 - \vec{n}\cdot (x, y, z) )\vec{n}$](/mathtex/a0/a07ee875d07141f9fe088f3b08c11256.gif) .
. s následnými úpravami.
s následnými úpravami.