Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 02. 05. 2015 19:41 — Editoval Brano (02. 05. 2015 19:47)
disjunktne intervaly
Ked uz sa nam tu rozbehli realne cisla, tak ma napadol takyto klasicky prikladik:
Dokazte, ze pre lubovolny system (po dvoch) disjunktnych intervalov v R je spocitatelny.
Bezny prvy napad je, ze kazdy interval obsahuje racionalne cislo a kedze su disjunktne, tak z kazdeho vyberiem ine cislo, ale tych moze byt iba spocitatelne vela. Lenze tento postup vyuziva axiomu vyberu a to je na dokaz spocitatelnosti "zbytocne" silne. Cize uloha je dokazat to bez axiomy vyberu.
Offline
#3 04. 05. 2015 01:51
Re: disjunktne intervaly
↑ Andrejka3:
mas pravdu, da sa to - a ano mal som na mysli ine riesenie, aj ked neviem ci krajsie, ale este chvilu to necham otvorene a potom napisem svoje riesenie.
Offline
#4 04. 05. 2015 17:10
- check_drummer

- Příspěvky: 5181
- Reputace: 106
Re: disjunktne intervaly
Ahoj,
nejsem schopen dohlédnout, zda níže uvedené nepoužívá axiom výběru:
"Máte úhel beta." "No to nemám."
Offline
#5 04. 05. 2015 17:23
Re: disjunktne intervaly
(najprv este na doplnenie - myslel som samozrejme nedegenerovane intervaly, ale to asi vsetci aj tak pochopili)
↑ check_drummer:
takto som to myslel aj ja - mozno trochu uhladenejsie by sa to dalo napisat takto
Offline

 je system disjunktych intervalov na
je system disjunktych intervalov na 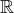 a nech
a nech 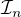 su tie z nich co maju dlzku aspon
su tie z nich co maju dlzku aspon 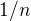 a neprazdny prienik s
a neprazdny prienik s 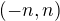 potom
potom 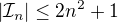 a
a 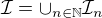 a teda je spocitatelny.
a teda je spocitatelny.