Matematické Fórum

↑ maver:
Ahoj.

Rozumím tomu tak, že:

1)  máme varietu W1 =  [A1, V1]   procházející bodem A1 a mající zaměření V1
(mohli bychom zavést třeba i pojem "směrový prostor variety W1")  , 

2)  máme varietu W2 =  [A2, V2]   procházející bodem A2 a mající zaměření V2 ,

3)  průnikem prostorů V1, V2  je prostor V3  generovaný vektorem  (1,-1,0,1).

Hledáme bod A3  takový, aby varieta  W3 = [A3, V3] (jakožto množina bodů)  byla průnikem variet  W1,  W2
(jakožto množin bodů).

Princip řešení: Bodem A3  může být kterýkoliv bod průniku variet  W1,  W2 (jakožto množin bodů).

Nevím, jakou terminologii jste si zavedlii, ale mám dojem, že pojem "varieta" používáš ve dvou odlišných významech -
někdy pro jistou množinu BODŮ a jindy pro jistou množinu VEKTORŮ (která s tou první množinou sice nějak souvisí,
ale totožná s ní není).

↑ maver:

Nejprve připomenu některá základní fakta.
Symbolem značíme množinu všech uspořádaných n-tic 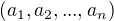  reálných čísel. Každou takovou usp. n-tici
můžeme geometricky interpretovat dvojím způsobem:

a) jako BOD,

b) jako VEKTOR (vyjadřujéící operaci posunutí) .

Mohli bycho zavést dvojí označení množiny podle toho, zda máme na mysli množinu bodů či množinu vektorů,  ale ne vždy
se to tak dělá, což může studentům činit potíže.

Lineární varieta jakožto množina BODŮ prostoru (mající vlastnosti specifické pro varietu) je určena dvěma faktory:

1) některým svým BODEM,
2) některým podprostorem vektorového prostoru , s nímž je varieta rovnoběžná -  tento podprostor se nazývá zaměření variety.

Příklady:

1. Množina obsahující právě jeden bod ji lin. varietou, jejímž zaměřením je podprostor dimense 0 (obsahující pouze nulový vektor).

2. Přímka je určena bodem, jímž prochází, a podprostorem dimense 1 (tedy jedním nenulovým vektorem), s nímž je rovnoběžná.

3. Rovina je určena bodem, jímž prochází, a podprostorem dimense 2 (tedy dvojicí lin. nezávislých vektorů), s nímž je rovnoběžná.

4. Lin. varieta procházející bodem [0, ...,. 0]  (počátkem soustavy souřadnic) je jakožto podmnožina v   totožná se svým zaměřením.

Průnik dvou lin. variet je buďto prázdný, nebo je to opět lin. varieta, jejímž zaměřením je průnik V podprostorů, které jsou zaměřeními
výchozích variet.  Nicméně určit pouze prostor V nestačí, je potřeba najít aspoň jeden společný BOD obou výchozích variet, tedy vyřešit 
vhodnou soustavu lin. rovnic - obdobně jako v té druhé úloze.