Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » vyšetřévání grafu funkce s absolutní hodnotou
#1 09. 05. 2015 20:53 — Editoval ragulin (09. 05. 2015 20:53)
vyšetřévání grafu funkce s absolutní hodnotou
Zdravím , čím víc hlouběji se dostávám do příkladů vyšetřévání grafu fce s logaritmy, tím víc zabředávám do problémů a neznalostí základů...
Podle mé logiky postupuji následovně:
1) Zjistím nulové body absolutní hodnoty a na vzniklých intervalech vyšetřím znaménka...dostávám
Na tomto intervalu se průsečíky
průsečíky
a 

Za B) 
Na tomto intervalu  průsečiky :
průsečiky :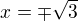

a za C)
Na tomtu intervalu 

Dále bych měl řešit asymptotu, tu to mít nebude, přecházím k limitám v krajních bodech...počítám takhle :


Ovšem vím, že mám někde chybu, jelikož okolo mínus dvojky by to mělo být z obou stran do mínus nekonečna...nejsem si vůbec jistý svým postupem....poradil by mi někdo prosím? Děkuji
Offline
#2 10. 05. 2015 08:29
Re: vyšetřévání grafu funkce s absolutní hodnotou
Neviem kde je problem limita x->-2 x^2 - 4 = 0 jasne ze este zalezi z ktorej strany
ked je lim h->0 ln(h) =-inf. Ale to len v pripade ze je to plus nula v tej druhej to je nedefinovane v R
toto mas v zavere ale zadani je s absolutnou hodnotou a tak v obydvoch nulach je - nekonecno
Offline
#3 10. 05. 2015 12:48
Re: vyšetřévání grafu funkce s absolutní hodnotou
↑ mates.dz:
Když vezmu tu druhou
A dosadím do ní číslo zleva od mínus dvojky, takže například -3...dostávám plus nekonečno....ale mělo by to být mínus ...
Offline
#4 10. 05. 2015 15:46 — Editoval Al1 (10. 05. 2015 16:25)
Re: vyšetřévání grafu funkce s absolutní hodnotou
↑ ragulin:
Zdravím, , dosazujeme číslo blízké (-2) zleva, tedy např. (-2,01); -3 je hrozně daleko.
, dosazujeme číslo blízké (-2) zleva, tedy např. (-2,01); -3 je hrozně daleko.
Dále v intervalu (-2;2) platí 
 , dosazujeme např. (-1,99)
, dosazujeme např. (-1,99)
A pak ještě " Dále bych měl řešit asymptotu, tu to mít nebude," z čeho soudíte? Pokud existuje aspoň jedna jednostranná nevlastní limita v bodě a, pak existuje asymptota bez směrnice x=a.
Offline
#5 10. 05. 2015 15:55
Re: vyšetřévání grafu funkce s absolutní hodnotou
↑ ragulin:
Mala otazka:
Co znamena pre teba: vysetrite funkciu....
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 10. 05. 2015 16:33 — Editoval vanok (10. 05. 2015 16:35)
Re: vyšetřévání grafu funkce s absolutní hodnotou
Vysetrit funkciu f, znamena minimalne
Urcit domenu definicie Df
Limity vo hranicnych bodoch Df+ asymptoty + relatif à pozicia kryvky a grafu funkcie
Spojitost funkcie
Variacie funkcie
Dérivatelnost
Extema
Konkavitu, konvexitu
Graf, aj zo zaujimavimi bodmy.
A ine ak si to zela vas profesor
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 10. 05. 2015 16:49
Re: vyšetřévání grafu funkce s absolutní hodnotou
↑ ragulin:
Důležité je, že  je maličko kladné a my počítáme logaritmus takové hodnoty. A z průběhu fce y=ln(x) plyne, že
je maličko kladné a my počítáme logaritmus takové hodnoty. A z průběhu fce y=ln(x) plyne, že 
Offline
#10 10. 05. 2015 17:02
Re: vyšetřévání grafu funkce s absolutní hodnotou
↑ vanok:
Ano...jen mám prostě osobně problém s limitama...:-) obecně...
↑ Al1:
Děkuji, už je mi to jasné...jen doufám, že zbytek toho postupu, co jsem napsal, je správně...hlavně co se týče absolutní hodnoty na ruzných intervalech...dělám to tak, že jednoduše vezmu absolutní hodnotu v danym intervalu, a řešim tu funkci tak, jak na tom intervalu vypadá...
Offline
#11 10. 05. 2015 17:09
Re: vyšetřévání grafu funkce s absolutní hodnotou
↑ ragulin:
No, úplně správně vše není průsečík s x je pouze
průsečík s x je pouze ![kopírovat do textarea $[-\sqrt{5};0]$](/mathtex/50/50ee720082128f3f356ae8ca9ab89701.gif)
 průsečík s x je pouze
průsečík s x je pouze ![kopírovat do textarea $[\sqrt{5};0]$](/mathtex/b9/b9de11e651e1b425ce372437aadfc022.gif)
Hodně napoví také to, že fce je sudá (důkaz je na vás).
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » vyšetřévání grafu funkce s absolutní hodnotou
