Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#7 11. 05. 2015 22:35
Re: kuželosečky
Ahoj,
tak pokud má střed ležet na přímce 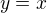 potom bude mít souřadnice
potom bude mít souřadnice ![kopírovat do textarea $S[n,n]$](/mathtex/01/014a0d399b935186ce4f0d960829a319.gif) jelikož všechny body na této přímce mají x-ovou souřadnici totožnou s y-ovou
jelikož všechny body na této přímce mají x-ovou souřadnici totožnou s y-ovou
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline




 ?
?
![kopírovat do textarea $(-a-b)^{2}=[(-1)\cdot (a+b)]^{2}=(-1)^{2}\cdot (a+b)^{2}=(a+b)^{2}$](/mathtex/40/40c4c1fc3054e2d4596c7ea29874dbf6.gif)