Matematické Fórum

tigerhell22 · 13. 05. 2015 09:46

Zdravim, mohl by mi někdo prosim Vás vysvětlit na nějakoým příkladu co přesně znamená entropie?
Našel jsem, že je to změna tepla k teplotě .. ale nějak nevim jak si to představit
Děkuji

Bati · 13. 05. 2015 10:37 — Editoval Bati (13. 05. 2015 11:00)

Ahoj,
vztah, který uvádíš je užitečný při výpočtech, ale je pravda, že se to přes něj těžko představuje. Jiný pohled na entropii měl Boltzmann. Vezmi nádobu s ideálním plynem. Snadno můžeme změřit veličiny jako objem, tlak, teplota... - tyto hodnoty určují makroskopický stav systému a stačí mi znát 3 z nich abych dopočítal všechny ostatní. Teď se na ten plyn budu dívat jako na seznam atomů, ke kterým si poznamenám jejich polohu a rychlost. Takto jsem teoreticky schopen zaznamenat každou konfiguraci (mikrostav) systému, ovšem množství informace, které zaznamenávám je obrovské (jeden mikrostav můžu ztotožnit s 6N-složkovým vektorem, kde N je počet částic). Dá se proto čekat, že jednomu makrostavu bude odpovídat obrovské množství mikrostavů. To, kolik jich je na jeden makrostav odpovídá entropii - přesně je to logaritmus z počtu mikrostavů krát boltzmannova konstanta.

Na entropii se tedy dá pohlížet takto: Představme si, že máme nějaký systém se složitou vnitřní sktrukturou, u kterého jsme schopni sledovat jen nějaké makroskopické vlastnosti. Entropie pak měří to, kolika způsoby můžu strukturu toho systému přeuspořádat, abych nezaznamenal žádnou makroskopickou změnu.

Ještě k té teplotě...my sice umíme něco naměřit teploměrem, ale nevíme, co to vlastně měříme, protože v systému může mezitím docházet k nejrůznějším procesům, které nevidíme a ovlivňují to, co měříme (systém není v termodynamické rovnováze). Proto se teplota definuje pomocí entropie.

Brzls · 13. 05. 2015 10:48 — Editoval Brzls (13. 05. 2015 11:01)

↑ tigerhell22:
Čau

Co je to entropie se tu řešilo již několikrát. Je zajímavé, že tato veličina dělá takové problémy.
Podle mě je nejlepší vnímat entropii pouze jako pomocný matematický pojem. Díky ní se nám spoustu teoretických vztahů zjednoduší a nebo se nám díky ní lépe některé teorie vytváří.

Jako takový ukázkový příklad bych zvolil výpočet účinnosti Carnotova cyklu.
Z definice entropie máme, že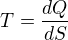
$T=\frac{dQ}{dS}$
tedy když určíš diferenciál tepla při nějakém konkrétním ději a tento přírůstek vydělíš teplotou, tak dostaneš diferenciál entropie. Integrací by si dostal vztah pro entropii.

Při izotermickym ději pak tedy nutně platí, že 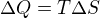$\Delta Q=T\Delta S$

Jelikož entropie je veličina stavová, tak je její změna při izotermické kompresi stejná jako při izotermické expanzi. Při adiabatických dějích je zřejmě změna entropie nulová. Platí tedy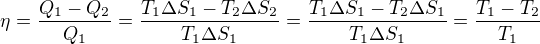
$\eta =\frac{Q_{1}-Q_{2}}{Q_{1}}=\frac{T_{1}\Delta S_{1}-T_{2}\Delta S_{2}}{T_{1}\Delta S_{1}}=\frac{T_{1}\Delta S_{1}-T_{2}\Delta S_{1}}{T_{1}\Delta S_{1}}=\frac{T_{1}-T_{2}}{T_{1}}$

On je význam entropie spíš teoretický, nenajdeš moc "praktických" příkladů, kde by si entropii využil.

↑ Bati:

Entropie pak měří to, kolika způsoby můžu strukturu toho systému přeuspořádat, abych nezaznamenal žádnou makroskopickou změnu

Když na to půjdu statisticky, tak vím, že platí
$S=-k\sum_{}^{}w_{n}\ln w_{n}$ kde wn je pravděpodobnost realizace n-tého stavu
(při spojitém rozdělení by to bylo trochu jinak, jen se mi nechtělo přemýšlet jak)

Jak z tohoto plyne ta věta, kterou si napsal? Tyhle různé vysvětlení entropie jsem já osobně nikdy nepochopil odkud se vzaly, prostě to v tom nevidím

Bati · 13. 05. 2015 11:05 — Editoval Bati (13. 05. 2015 11:20)

↑ Brzls:
Ahoj,
tvůj přístup má právě trochu háček v tom, že vztah 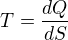$T=\frac{dQ}{dS}$ obsahuje 2 veličiny, které potřebuješ definovat - teplotu a entropii - viz můj edit. Jakmile ale jedno z toho máš, lze se na entropii opravdu dívat jako na "pomocnou matematickou veličinu", která usnadňuje počítaní.

Ta věta vychází z představy entropie jako míry toho, kolikrát je víc mikrostavů než makrostavů, přičemž pokud bych to chtěl říct přesně, musel bych zde popsat Boltzmannovo rozdělení. Ta tvoje formule pro S je jen středování mé formule přes všechny stavy.

Brzls · 16. 05. 2015 12:30

↑ Bati:

Tak ono v klasické termodynamice se skutečně teplota zavádí různými způsoby (pomocí ideálního plynu, roztažnosti látek, Carnotova cyklu...) jenže je patrné, že je to takové krkolomné a působí to složitě, uměle, nematematicky. Poté se postuluje existence stavové veličiny entropie pomocí toho vztahu a ani není potřeba nějak mluvit o tom, co to je.

Ze statistické fyziky znám jenom hrubý základ (chtěl jsem si umět pořádně odvodit stavovou rovnici), resp jsem hlavně čerpal z tohoto http://www.aldebaran.cz/studium/statistika.pdf

jenže zde je teplota už nějak tak předem mlčky definována, tedy podle toho, co píšeš ty, tak celá ta teorie není vypracována od úplných základů.

Je nějaký dostupný zdroj, kdy by byl ten pohled na entropii vysvětlený?

Bati · 16. 05. 2015 16:00

↑ Brzls:
Zavést nějakou stupnici v konkrétních případech můžeme, ale nevíme, jestli měříme vždycky to samé. V Kvasnicovi jistě bude teplota zavedená pořádně, ale nevím teď jestli přes entropii.
Odkaz: http://uloz.to/xaVn6St7/tsf-kvasnica-pdf

Na str. 35, kde začíná teplota se hned v úvodu píše, to, na co tady narážím:

Pojem teploty je jedním z nejdůležitějších fyzikálních pojmů. V úvodním kursu fyziky se pojem teploty zpravidla zavádí na základě některých speciálních vlastností látek (jako jsou objemová roztažnost, rozpínavost apod.). Při tomto názorném postupu (většinou nutném v úvodních přednáškách) se však ztrácí obecnost pojmu teploty a oblast jeho použití. ... přejdeme přímo k obecnému zavedení teploty jako stavové veličiny na základě některých obecných vlastností systémů v termodynamické rovnováze.

Matematické Fórum

#1 13. 05. 2015 09:46

Entropie

#2 13. 05. 2015 10:37 — Editoval Bati (13. 05. 2015 11:00)

Re: Entropie

#3 13. 05. 2015 10:48 — Editoval Brzls (13. 05. 2015 11:01)

Re: Entropie

#4 13. 05. 2015 11:05 — Editoval Bati (13. 05. 2015 11:20)

Re: Entropie

#5 16. 05. 2015 12:30

Re: Entropie

#6 16. 05. 2015 16:00

Re: Entropie

Zápatí