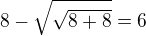Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 12. 03. 2014 20:53
Série jednoduchých hádanek
Zdravím,
zrovna nedávno jsem narazila na sérii matematických příkladů, které mě nadchly natolik, že se o ně s vámi musím podělit.
Cílem je s použitím libovolného počtu jakýchkoli matematických operací dospět ke kýženému výsledku, ve všech případech číslu 6.
1 1 1 = 6
2 2 2 = 6
3 3 3 = 6
4 4 4 = 6
5 5 5 = 6
6 6 6 = 6
7 7 7 = 6
8 8 8 = 6
9 9 9 = 6
Pro ilustaci vyřeším ten s dvojkami → 2 + 2 + 2 = 6
Tak co, podařily se vám všechny? No že se vůbec ptám :)
Offline
#2 12. 03. 2014 22:32
Re: Série jednoduchých hádanek
Ahoj ↑ Xantippa:,
zabavne...
Aj pre 3 10 je riesenie:
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 29. 04. 2015 18:23
Re: Série jednoduchých hádanek
Ahoj ↑ Xantippa:
Hodil jsem na GeoGebru řešení. http://tube.geogebra.org/student/m1104929
Akorát doufám, že je povolena třetí odmocnina jinak si nevím rady s osmičkami.
Přidal jsem tam i řešení pro tři nuly :)
Na závěr Vás zde na fóru všechny zdravím. Jsem tu poprvé.
ahoj, Honza
GeoGebra 5.0.119.0 22 May 2015 Java 1.7.0_40-32bit
Offline
#5 13. 05. 2015 01:00 — Editoval Kondr (13. 05. 2015 01:06)
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4247
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Série jednoduchých hádanek
Pokud se smí zaokrouhlovací funkce, tak pro k>3 
Pokud se smí třetí odmocnina, tak pro k>1 ![kopírovat do textarea $\log_{\sqrt[3]{k}}(k\cdot k)=6$](/mathtex/ba/ba7e4fb00fe561e981e3defa489f39a8.gif)
Jinak jsem našel zadání, které povoluje jen +,-,*,/,!, a druhou odmocninu -- to stačí i pro osmičku.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#6 13. 05. 2015 19:49 — Editoval check_drummer (13. 05. 2015 19:51)
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Série jednoduchých hádanek
↑ Xantippa:
Ahoj, co je to "jakákoliv matematická operace"? Např. definuju si operaci x*y=6 pro libovolná x,y a pak je řešením všech úloh x*y*z=6. :-)
"Máte úhel beta." "No to nemám."
Offline
#7 25. 05. 2015 15:20 — Editoval JanKnot (25. 05. 2015 15:31)
Re: Série jednoduchých hádanek
↑ check_drummer:
Dle mého názoru je hádanka myšlena tak, že s použitím třech stejných celých čísel ... atd. Proto jsem zmiňoval osmičky a třetí mocninu. Narozdíl od druhé se u třetí píše trojka a tím pádem by mé řešení osmiček nabylo regulérní. Respektive bylo ale jen ve strojovém jazyku (cbrt(8) + cbrt(8) + cbrt(8)).
GeoGebra 5.0.119.0 22 May 2015 Java 1.7.0_40-32bit
Offline
#8 25. 05. 2015 18:16
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Série jednoduchých hádanek
↑ JanKnot:
Ale moje operace je definovány pro tři čísla... Resp. pro dvě a tedy zřetězením i pro tři.
"Máte úhel beta." "No to nemám."
Offline
#9 25. 05. 2015 22:26 — Editoval JanKnot (25. 05. 2015 22:37)
Re: Série jednoduchých hádanek
↑ check_drummer:
Jasně. Abstraktnímu myšlení se meze nekladou :) Jen jsem tím naznačoval, že při každé hádance nebo třeba hře je třeba si stanovit nějaká pravidla. Jinak by šlo obejít leccos. Já si stanovil takové jak jsem napsal a Ty zase své. Není mezi námi sporu. Jen rozdílný pohled na věc.
Mimochodem, nevíš jak jinak ty osmičky? Bez použití třetí odmocniny? Já nevím... Prostě aby se v příkladu vyskytovaly jen tři osmičky a žádné jiné číslo.
GeoGebra 5.0.119.0 22 May 2015 Java 1.7.0_40-32bit
Offline


![kopírovat do textarea $n\ge1,\forall k\in\{3^n+1,3^n+2,\ldots,4^n-1,4^n\}:\(\left\lfloor\sqrt[n]{k-\frac{k}{k}}\right\rfloor\)!=6$](/mathtex/f9/f93b07ff606394b9337dfa328509957e.gif)