Matematické Fórum

Crashatorr · 30. 05. 2015 22:17

Zdravím, mohl bych někoho poprosit o vysvětlení Riemannovy metriky?

Nechť $g:\mathbb{R}^{m}->\mathbb{R}$ potom Riemannovou metrikou rozumíme tuto pozitivně definitní kvadratickou formu $\sum_{i,j=1}^{m}g_{i,j}dx_{i}dx_{j}$

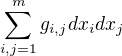
Moc nevím co si pod touto definicí představit, byl by někdo ochotný to trochu zjednodušit, popřípadě vysvětlit na nějakém příkladě?

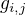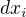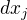Mám napsané že $g_{i,j}$ jsou funkce $\mathbb{R}^{m}->\mathbb{R}$ , $dx_{i}$ a $dx_{j}$ jsou funkce, které vektoru u přiřadí jeho i-tou resp. j-tou složku

Jj · 31. 05. 2015 11:07 — Editoval Jj (31. 05. 2015 11:08)

↑ Crashatorr:

Dobrý den.

Vámi uvedený vztah v podstatě znamená čtverec vzdálenosti dvou blízkých bodů v prostorech s Riemannovou metrikou.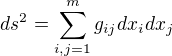

$ds^2 = \sum_{i,j=1}^{m}g_{ij}dx_{i}dx_{j}$
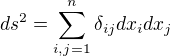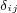Např. v Eukleidovském prostoru En (nejjednodušší případ Riemannova prostoru) platí $ds^2 = \sum_{i,j=1}^{n}\delta_{ij}dx_{i}dx_{j}$ , kde $_{\delta_{ij}}$ je Kroneckerovo delta.

Ve sférických souřadnicích na povrchu koule o poloměru R: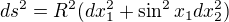

$ds^2=R^2(dx_1^2+\sin^2 x_1 dx_2^2)$

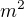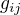$m^2$ čísel $g_{ij}$ tvoří složky tzv. metrického tenzoru: $gij=\begin{pmatrix} R^2 & 0 \\ 0 & R^2\sin^2 x_1 \end{pmatrix},\quad i,j \in \langle 1,2 \rangle$

Crashatorr · 31. 05. 2015 11:19

↑ Jj:
Díky za odpověď, musím se však přiznat, že o moc chytřejší nejsem.
Pokud jsem pochopil správně ten základ tak 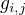$g_{i,j}$ se změní pokaždé když se po tom prostoru někam posuneme, tudíž se asi v každém bodě bude metrika počítat jinak, nějak teda nedokážu strávit to že jak můžeme podle toho měřit když pokaždé se metrika spočítá jinak

Matematické Fórum

#1 30. 05. 2015 22:17

Riemannova metrika

#2 31. 05. 2015 11:07 — Editoval Jj (31. 05. 2015 11:08)

Re: Riemannova metrika

#3 31. 05. 2015 11:19

Re: Riemannova metrika

Zápatí