Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 31. 05. 2015 21:26 — Editoval Al1 (31. 05. 2015 21:27)
Re: Definiční obor
↑ Martin95:
Zdravím,
logaritmus se základem 1/3 je skutečně klesající fce. To má vliv na řešení nerovnice
Offline

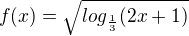 ,
, , ale také platí, že
, ale také platí, že