Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematických struktur
- » Racionální a iracionální čísla (TOTO TÉMA JE VYŘEŠENÉ)
#1 24. 04. 2015 15:12
Racionální a iracionální čísla
Zdravím,
již dlouhou dobu jsem se pokoušel dokázat větu, že mezi libovolnými dvěma reálnými čísly  existuje nekonečně mnoho racionálních i iracionálních čísel. Myslím, že se mi to konečně podařilo (i když stoprocentně jistý si nejsem). Chtěl bych poprosit o komentář, kde se v důkazu nachází slabiny (ať už faktické, nebo pouze formální). Další dotaz, jde to udělat nějak (úplně(?)) jinak?
existuje nekonečně mnoho racionálních i iracionálních čísel. Myslím, že se mi to konečně podařilo (i když stoprocentně jistý si nejsem). Chtěl bych poprosit o komentář, kde se v důkazu nachází slabiny (ať už faktické, nebo pouze formální). Další dotaz, jde to udělat nějak (úplně(?)) jinak?
Děkuji za reakce.
http://goo.gl/Hed7CY
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
- (téma jako vyřešené označil(a) byk7)
#2 24. 04. 2015 18:09
Re: Racionální a iracionální čísla
Ahoj ↑ byk7:,
Tvoj dokaz ked budem mat cas podrobnejsie pozriet.
Ina technika:
Staci dokazat ze lubovolny otvoreny interval I=]a,b[, a<b je bijectivny z R.
Inac v tvojom dokaze ukazujes ze pocet iraciolnych cisiel v nejakom intervale je nekonecny spocitatelny, ale tych je v tvojom intervale o mnoho viac.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 24. 04. 2015 22:38
Re: Racionální a iracionální čísla
Ahoj,
Veta co dokazujes, sa da vyjadrit aj takto: je huste v
je huste v 
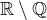 je huste v
je huste v  .
.
Ak chces pridam moj dokaz, aby si mohol porovnat.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 24. 04. 2015 22:44
Re: Racionální a iracionální čísla
↑ vanok:
Pojmu "hustá množina" jsem se chtěl vyhnout, protože používá topologické termín termíny, čemuž já zatím nerozumím.
Rád si Váš důkaz prohlédnu. :)
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#6 25. 04. 2015 12:40 — Editoval check_drummer (25. 04. 2015 12:41)
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Racionální a iracionální čísla
↑ byk7:
Ahoj, pdole mého stačí dk, že v každém intevalu I:=(a,b) se nachází alespoň jedno racionální a alespoň jedno iracionální číslo. Potom tedy např. je-li toto číslo x, tak stejný postup aplikujeme např. na interval (a,x) a tak získáme nekonečně mnoho požadovaných čísel.
Důkaz výše uvedeného tvrzení pro racionální x by mohl být např. takový, že lze nalézt u z Q dostatečně blízké k 0 (např. u=1/n pr odostatečně velké n) a je-li jeho velikost menší než délka I, tak vhodným celočíselným násobkem u získáme číslo z I.
Pro x iracionální lze použít tentýž postup (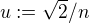 ).
).
"Máte úhel beta." "No to nemám."
Offline
#7 25. 04. 2015 12:59
Re: Racionální a iracionální čísla
Ahoj,
Pred tym ako tu dam dokazy, co som slubil, dam do popredia tuto poznamku.
Casto ked sa robia dokazy, kde  je dolezite vediet, ze sa v nich objavia ( nemo) prvky topologie, ( vsak
je dolezite vediet, ze sa v nich objavia ( nemo) prvky topologie, ( vsak  je model, co sa tyka zaciatkov topologie).
je model, co sa tyka zaciatkov topologie).
Inac, tiez iste vies, ze struktura  sa da vybudovat viacerymi sposobmi. Pochopitelne treba vzdy dokazat ze kazda konstrukcia je ekvivalentna z kazdou inou konstrukciou. Preto je sa
sa da vybudovat viacerymi sposobmi. Pochopitelne treba vzdy dokazat ze kazda konstrukcia je ekvivalentna z kazdou inou konstrukciou. Preto je sa  casto uvadza axiomaticky. (Aj na to je viacej presentacii )
casto uvadza axiomaticky. (Aj na to je viacej presentacii )
A na koniec este jedna poznamka.
Jedna dolezita axioma v  je Archimedova vlasnost.
je Archimedova vlasnost.
Povieme, ze  je archimedovske:
je archimedovske:
Pre kazde realne x, existuje prirodzene n ostro vädcie ako x.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 25. 04. 2015 21:42 — Editoval vanok (26. 04. 2015 11:51)
Re: Racionální a iracionální čísla
Pre istotu male upresnenia je huste v
je huste v 
Znamena:lubovolny otvoreny ( neprazdny) interval z  obsahuje nekonecne vela racionalnich cisiel.
obsahuje nekonecne vela racionalnich cisiel.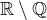 je huste v
je huste v  .
.
Znamena:lubovolny otvoreny ( neprazdny) interval z  obsahuje nekonecne vela irracionalnich cisiel
obsahuje nekonecne vela irracionalnich cisiel
Teraz dokazem v 3ch castiach co som vyssie slubil.
Predpokladajme ze 
1. Kazdy internal ]a,b[obsahuje aspon jedno racionalne cislo.
Co sa formalne pise
Myslienka dokazu je najst racionalne cislo  , kde
, kde 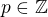 a
a 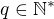 , cize teba najst take
, cize teba najst take 
Cize treba nast 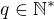 ze interval
ze interval ![kopírovat do textarea $]qa, qb[$](/mathtex/ce/ced4cdff93cb90d7a9b3778f47e81e9e.gif) obsahuje cele
obsahuje cele  .
.
Na to staci, ze dlzka  , co je ekvivalentne z
, co je ekvivalentne z 
Toto nas doviedlo, vdaka Archimedovej vlasnosti k tomutu dokazu.
Existuje cele  take, ze
take, ze  . Akoze
. Akoze  , mame
, mame  . Polozme
. Polozme ![kopírovat do textarea $p=[aq]+1$](/mathtex/a6/a6c81902ea1b5110c137f97ab428ebb2.gif) .
.
Preto  .
.
To nam da  , ako aj
, ako aj 
Cize  .
.
To nam konecne da ![kopírovat do textarea $\frac pq \in ]a, b[$](/mathtex/69/69a1b636c110c0ad909f45af201ade15.gif) co ukoncuje dokaz casti 1.
co ukoncuje dokaz casti 1.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 26. 04. 2015 11:38 — Editoval vanok (26. 04. 2015 18:56)
Re: Racionální a iracionální čísla
2. Kazdy otvoreny( neprazdny) interval obsahuje aspon jedno iracionalne cislo.
Pouzijem, cast 1. V intervaly ![kopírovat do textarea $ ]a-\sqrt 2, b-\sqrt 2[$](/mathtex/53/53c66d6ce30cabd35e5a5e8184859743.gif) existuje rationalne cislo
existuje rationalne cislo  .
.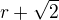 je iracionalne a je v
je iracionalne a je v ![kopírovat do textarea $]a,b[$](/mathtex/d2/d2cfa92d023d6064643fc246cc8a89b8.gif) ( vdaka posunutiu )
( vdaka posunutiu )
Posledna cast
3. Kazdy otvoreny( neprazdny) interval obsahuje nekonecne vela rationalnich a iracionalnich cisiel.
Staci konstatovat, ze ![kopírovat do textarea $I=]a,b[$](/mathtex/de/de86131a120979b094f75082521be5fe.gif) obsahuje
obsahuje  kde
kde  disjoinktnich otvorenich intervalov a na kazdy pouzit vlasnoti 1. a 2.
disjoinktnich otvorenich intervalov a na kazdy pouzit vlasnoti 1. a 2.
Cize 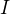 obsahuje aspon
obsahuje aspon  ,
, 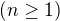 racionalnich a iracionalnich cisiel. Toto plati pre kazde
racionalnich a iracionalnich cisiel. Toto plati pre kazde 
To konci dokaz 3.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#11 30. 05. 2015 02:03
Re: Racionální a iracionální čísla
↑ vanok:
Ako z faktu, že v intervale ![kopírovat do textarea $[a,b]$](/mathtex/4a/4ab4b4c56d5423829b45e9ed06c42c5b.gif) je
je  racionálnych a
racionálnych a  iracionálnych čísel plynie, že je tam nekonečne veľa racionálnych a zároveň nekonečne veľa iracionálnych čísel ?
iracionálnych čísel plynie, že je tam nekonečne veľa racionálnych a zároveň nekonečne veľa iracionálnych čísel ?
1^6 - 2^6 + 3^6 = 666
Offline
#12 30. 05. 2015 02:11
Re: Racionální a iracionální čísla
Ahoj ↑ BakyX:,
Klucove slovo je indukcia.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#13 30. 05. 2015 02:44
Re: Racionální a iracionální čísla
↑ vanok:
Mohol by si to prosím rozpísať ?
Existuje ľubovoľne dlhá postupnosť po sebe idúdich zložených čísel, ale nie nekonečne dlhá.
Prečo by to nemohol byť tento prípad ?
1^6 - 2^6 + 3^6 = 666
Offline
#14 30. 05. 2015 07:26
Re: Racionální a iracionální čísla
↑ BakyX:
Neformalne
Indukcny krok.
Tu mozes pouzit, zéro ak mas k intervalov, mozes z nich vybrat lubovolny z nich, akoze tento obsahuje aspon jedno rationalne cislo, dostaneme dva ( mensie) disjoinktne intervaly. Na kazdy z nich mozes applikovat bod 1 a 2. To da, k +1 disjointnich intervalov ... z ktorych kazdy obsahuje aspon jedno rationalne ako aj irationalne cislo.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#15 30. 05. 2015 14:47
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Racionální a iracionální čísla
↑ BakyX:
Ahoj, stačí dokonce jedno, viz můj příspěvek.
"Máte úhel beta." "No to nemám."
Offline
#16 30. 05. 2015 19:28
Re: Racionální a iracionální čísla
Ahoj ↑ check_drummer:,
Vsak v principe pises to iste ako ja. Az nato ze som dal viac detailov.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#18 01. 06. 2015 12:33
Re: Racionální a iracionální čísla
Poznamka:
Ak chcete ine dokazy ( skor redakcie dokazu) dajte si na Google : density of Q.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematických struktur
- » Racionální a iracionální čísla (TOTO TÉMA JE VYŘEŠENÉ)
