Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 01. 06. 2015 15:48
Jordanov tvar podrobne - pre každý prípad
Dobrý deň,
skoro všade sa vyskytujú matice, pre ktoré sa dajú jednoducho vypočítať jordanove tvary aj s bázami, avšak neviem nájsť na internete príklady podobné naším testom, kde mi vlastné vektory nedajú dosť informácií na zostavenie bázy P. Ako príklad uvádzam túto maticu:
Vlastné čísla spočítam ako
a teda vlstné čísla sú 
Potom by som vypočítal vlastné vektory ako N(A-1E), N(A+1E) prípadne 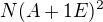 a
a 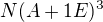 . (E je jednotková matica)
. (E je jednotková matica)
a teda pre N(A-1) výjde 
a pre N(A+1E) výjde  a
a  ,
,
čo aj keby bolo správne sú len tri vektory a mi na obloženie jordanovho tvaru potrebujeme 4 a taktiež si nie som istý ako bude vyzerať ten jordanov tvar.
Offline
#2 04. 06. 2015 11:24 Příspěvek uživatele Andrejka3 byl skryt uživatelem Andrejka3. Důvod: chyba, opravim
#3 04. 06. 2015 12:30 — Editoval Andrejka3 (04. 06. 2015 12:31)
Re: Jordanov tvar podrobne - pre každý prípad
↑ peeeto:
Ahoj.
Algebraická násobnost vl č 1 je jedna (násobnost char. polynomu), stejně tak jako geometrická násobnost (dimenze jádra A-E). Tímto jsme vyřešili invariantní podprostor příslušný vlastnímu číslu 1.
Vl. č. -1 má alg násobnost 3, kdežto, jak jsi zjistil, geometrickou pouze 2. To znamená, že struktura zobecněného podprostoru pro -1 je následující:
a
|
c b
kde a,b,c je base N(A-E)^2, b,c je base N(A-E), navíc 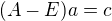 . Říká se tomu řetízky - jeden je délky dva, jeden délky jedna.
. Říká se tomu řetízky - jeden je délky dva, jeden délky jedna.
Je tedy třeba najít nějaký prvek z 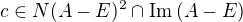 , najít k němu vzor v A-E,
, najít k němu vzor v A-E,  , a doplnit k c vektor b tak, aby b,c byla base N(A-E). To zde není tak těžké, půjdeme na to trikem -- nejdřív si zvolíme
, a doplnit k c vektor b tak, aby b,c byla base N(A-E). To zde není tak těžké, půjdeme na to trikem -- nejdřív si zvolíme  .
.
Base 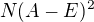 je
je 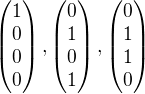 , přičemž je vidět, že ten druhý vektor není v N(A-E). Tak si označme
, přičemž je vidět, že ten druhý vektor není v N(A-E). Tak si označme  .
.
Pak 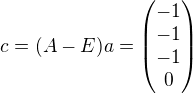 a k
a k  přidejme jeden vektor b tak, aby b,c byla base N(A-E). Lze volit
přidejme jeden vektor b tak, aby b,c byla base N(A-E). Lze volit 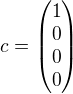 .
.
Nyní blok matice 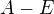 v invariantním podprostoru generovaném basí
v invariantním podprostoru generovaném basí 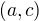 má tvar
má tvar  , tedy tento blok pro
, tedy tento blok pro  je
je  .
.
Celý Jordanův tvar je pak složením tří bloků: blok pro vl č 1, a dva pro -1.
What does a drowning number theorist say?
'log log log log ...'
Offline
