Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Obecná rovnice přímky kolmé na vektor (TOTO TÉMA JE VYŘEŠENÉ)
#1 07. 06. 2015 20:20
Obecná rovnice přímky kolmé na vektor
Otázka zní "Obecná rovnice přímky, která prochází středem kružnice 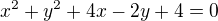 a je kolmá na vektor (3, r), kde r je poloměr kružnice, lze napsat ve tvaru:"
a je kolmá na vektor (3, r), kde r je poloměr kružnice, lze napsat ve tvaru:"
ať dělám co dělám, tak mi vychází 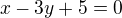 ale odpověď je
ale odpověď je  , takže na něco jsem asi určitě zapomněl, ale nemůžu najít co :-( předem děkuji za odpověď
, takže na něco jsem asi určitě zapomněl, ale nemůžu najít co :-( předem děkuji za odpověď
Offline
- (téma jako vyřešené označil(a) MrKaney)
#2 07. 06. 2015 20:27 — Editoval krauva (07. 06. 2015 20:29)
Re: Obecná rovnice přímky kolmé na vektor
↑ MrKaney:
přímka je kolmá na vektor, tudíž je to její normálový vektor (3, 1) a už ho nemusíš "kolmit" ;)
Offline
#3 07. 06. 2015 20:29
Re: Obecná rovnice přímky kolmé na vektor
↑ MrKaney:
Zdravím.
Středový tvar rovnice: 
Po úpravě dostaneš 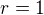
![kopírovat do textarea $S=[-2;1]$](/mathtex/7a/7aa0c3ba4a059fe69647f65adaca5ea3.gif)
Pak stačí udělat kolmý vektor k vektoru 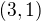
Sestavit parametrické rovnice přímky a z nich odstraněním parametru rovnici obecnou.
Offline
#5 07. 06. 2015 20:34 — Editoval krauva (07. 06. 2015 20:35)
Re: Obecná rovnice přímky kolmé na vektor
↑ Panassino:
a do rovnice za x a y dosadíš střed kružnice (leží na přímce) a dopočteš c
Offline
#7 07. 06. 2015 21:39
Re: Obecná rovnice přímky kolmé na vektor
↑ Panassino: Dobrý, chyba byla v tom, co podotkl(a) krauva, ale oběma děkuji za odpověď. :)
Offline
#8 07. 06. 2015 21:42
Re: Obecná rovnice přímky kolmé na vektor
Jenom bych se ještě rád zeptal: jak zjistím, že ten vektor je již normálový? Když vidím, že mám zjistit rovnici přímky, která je KOLMÁ na vektor, tak automaticky chci obracet čísla, i když očividně se to nemá, alespoň v tomhle případě.
Offline
#9 08. 06. 2015 00:27
Re: Obecná rovnice přímky kolmé na vektor
↑ MrKaney:
Pokud máš zjistit rovnici přímky, která je kolmá na vektor 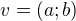 , pak to můžeš udělat dvěma způsoby, které jsou zmíněny výše. Můžeš najít směrový vektor přímky a bod, kterým přímka prochází, a sestrojíš parametrické rovnice, nebo využiješ normálový vektor a pomocí bodu, o kterém víš, že leží na přímce, najdeš parametr c.
, pak to můžeš udělat dvěma způsoby, které jsou zmíněny výše. Můžeš najít směrový vektor přímky a bod, kterým přímka prochází, a sestrojíš parametrické rovnice, nebo využiješ normálový vektor a pomocí bodu, o kterém víš, že leží na přímce, najdeš parametr c.
Obecná rovnice přímky: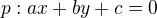 kde a,b,c jsou parametry.
kde a,b,c jsou parametry.
Normálový vektor této přímky: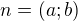
Směrový vektor (kolmý na normálový): 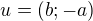
Je to jasnější?
Offline
#10 09. 06. 2015 11:54
Re: Obecná rovnice přímky kolmé na vektor
↑ Panassino: Toto vše právě chápu, ale v mém příspěvku je, že hledám obecnou rovnici přímky, která je kolmá na vektor (3,r), ale v důsledku jsme ten vektor nepřevraceli, a použili jsme vektor (3,r) tak jak je, i když hledáme přímku KOLMOU na ten vektor... Mě prostě nedochází, proč jsme ten vektor nepřevraceli, když se hledá rovnice kolmá na vektor
Offline
#11 09. 06. 2015 11:59
Re: Obecná rovnice přímky kolmé na vektor
↑ MrKaney:
Zdravím,
normálový vektor, který potřebuješ pro obecnou rovnici přímky, je každý vektor k přímce kolmý. Takže přímka kolmá na vektor má tento jako svůj normálový vektor. Namaluj si obrázek.
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » Obecná rovnice přímky kolmé na vektor (TOTO TÉMA JE VYŘEŠENÉ)