Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Didaktika a pedagogika: metodiky výuky a výukové materiály
- » Kuzelosecka 2
#1 09. 06. 2015 12:29
Kuzelosecka 2
Pozdravujem,
Ako ste definovali kuzelosecky v euklidovskom priestore ?
A ake vlasnosti ste potom mohli dokazat?
Na akej urovni, to bolo mozne?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#2 09. 06. 2015 13:31
Re: Kuzelosecka 2
Snad jsem vybral správné téma. :-)
My jsme kuželosečky definovali jako množiny bodů v rovině s jistou vlastností. Na základě této vlastnosti jsme pak odvodili rovnice těchto útvarů, byť jen ve speciální poloze.
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#3 10. 06. 2015 00:17 — Editoval vanok (10. 06. 2015 14:48)
Re: Kuzelosecka 2
Ahoj ↑ byk7:,
Mozes dat priklady takych vlasnosti?
Pre amaterov moznych definicii, v tomto ramci ( euklidovska rovina ) jedna casta definicia, na urovni prvy, pripadne druhy rocnik VS.
Nech je dany jeden bod  , jedna priamka
, jedna priamka  (
(  ) a cislo
) a cislo  , potom mnozina
, potom mnozina  bodov
bodov  roviny ktorich pomer vzdialenosti od bodu
roviny ktorich pomer vzdialenosti od bodu  à od priamky
à od priamky  je konstanta
je konstanta  :
:  definuje jednu kuzelosecku.
definuje jednu kuzelosecku. sa vola ohnisko
sa vola ohnisko smernica
smernica excentricita (iste by ste to uhadli, aj ked niektore cz, sk pramene o tom nechcu vediet)
excentricita (iste by ste to uhadli, aj ked niektore cz, sk pramene o tom nechcu vediet)
A 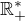 je mnozina nenulovych kladnych realnych cisiel.
je mnozina nenulovych kladnych realnych cisiel.
d(.,.) oznacuje dlzku.
Pridajte dalsie definicie, ktore ste stretli.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 10. 06. 2015 13:26 — Editoval misaH (10. 06. 2015 13:30)
- misaH
- Příspěvky: 13459
Re: Kuzelosecka 2
↑ vanok:
Ahoj, vanok.
Nerozumiem, čo vlastne riešiš.
Excentricita na Slovensku a (predpokladám) v Čechách ( na SŠ) je to, čo Ty voláš (asi) lineárna excentricita.
Ja som sa napríklad so žiadnou inou definíciu excentricity ani počas štúdia matematiky na VŠ nestretla.
No a čo?
"Správne" definície predsa neexistujú.
Nájsť definície kužeľosečiek sa na nete dajú bez problémov. Tak sa aj učia. Predpokladám, že kužeľosečky vyzerajú rovnako podľa Tvojej aj našej školskej definície.
Offline
#5 10. 06. 2015 14:18
Re: Kuzelosecka 2
↑ misaH:
Ahoj
Ja vobec nechcem polemizovat, kazdy si robi ako mysli. Ale konstatovat rozdiely, ak existuju, v terminologii sa mi zda uzitocne, aby pripadny citatel nebol strateny. Definicie maju casto aj ich historiu... a vediet o nej je zaujimave.
Co sa uci alebo nie, to je to co je uzitocne tu napisat... vsak tu ide o didaktiku.
Tak mozes napisat tvoj osobny vztah k tomu ako sa nieco vyucuje a lebo aj nevyucuje, a ake to ma, moze mat dopady.
Ze sa nieco najde na nete je zaujimave, no zial nie vsetko je vieruhodne.
Mozes tu napisat tvoje svedectvo, o tom ako by si konkretne videla uvedenie pojmu kuzelosecka v euklidovskej rovine, podla predpokladanej urovni na akej by si chcela pracovat ....
Co sa tyka definicii, je uz otvorene ine vlakno. Tak pis o tom tam ak chces nam povedat na tu temu zaujimave observacie.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 10. 06. 2015 14:40 — Editoval vanok (10. 06. 2015 22:48)
Re: Kuzelosecka 2
Pokracujem toto ↑ vanok:, tym, ze pridam mozny postup ako pokracovat v rozvoji uvedeneho pojmu.
Oznacme  kolmicu na smernicu
kolmicu na smernicu  ktora prechadza ohniskom
ktora prechadza ohniskom  . Tato priamka je pochopitelne osa symetrie
. Tato priamka je pochopitelne osa symetrie  . Budeme ju volat ohniskova (fokalna) osa kuzelosecky
. Budeme ju volat ohniskova (fokalna) osa kuzelosecky  .
.
Zoberme jeden ortonormalny reper  , kde
, kde  , potom mozme pisat karteziansku rovnicu priamky
, potom mozme pisat karteziansku rovnicu priamky  :
: 
Cize 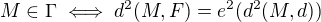
To nam da karteziansku rovnicu 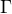 vo vybranom repere
vo vybranom repere  .
. 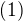
Kde  ma suradnice x,y vo vybranom repere.
ma suradnice x,y vo vybranom repere.
Teraz podla hodnot  mozme uviest rozne typy kuzeloseciek.
mozme uviest rozne typy kuzeloseciek.
Pripadne pokracovanie.....
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 10. 06. 2015 15:07
Re: Kuzelosecka 2
↑ vanok:
- přímka a bod, která na ní neleží -> množina bodů, která má od obou objektů stejnou vzdálenost -> parabola
- dva body -> množina bodů, která má konstantní součet vzdáleností od těch dvou daných -> elipsa
- dva body -> množina bodů, která má konstantní absolutní hodnotu rozdílu vzdáleností od těch dvou daných -> hyperbola
žádnou definici, která by kuželosečky sjednocovala, jsme si neuváděli
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#9 10. 06. 2015 22:59
Re: Kuzelosecka 2
Ahoj ↑ byk7:,
Na strednej skole to asi staci, no pre niekoho kto chce prehlbit je mozne ukazat, ako som to vyssie naznacil ↑ vanok:, ( cf. Relacia 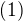 ) ze je mozne mat "zjednotenu" definiciu (a da sa ukazat ze su aj ine moznosti) ....
) ze je mozne mat "zjednotenu" definiciu (a da sa ukazat ze su aj ine moznosti) ....
Ked budem mat trochu casu, pridam (alebo aspon naznacim) ti tu ako vdaka definicii, co som pripomenul, mozes prist k rovniciam ktore su tiez charakterizuju kuzelosecky.( co ste pochopitelne aj vy dokazali, a takto budeme moct byt isti, ze hovorime o tom istom. 😄)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1
- Hlavní strana
- » Didaktika a pedagogika: metodiky výuky a výukové materiály
- » Kuzelosecka 2
