Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 16. 06. 2015 19:10
- anicka3112

- Zelenáč
- Příspěvky: 9
- Reputace: 0
Geometrie
Prosím, potřebuji poradit s tímto příkladem. Potřebuji výsledek, i s postupem, jelikož si nedokážu dosadit do vzorce čísla. Je dán pravouhly trojuhelnik ABC, s pravým úhlem při vrcholu C. Strana b =5cm, ta=7,2 cm. Výpočtem dokažte, že obsah rovnostranného trojuhelníku sestrojeného nad přeponou, se rovná součtu obsahů rovnostranných trojuhelníků sestrojenými nad oběma odvěsnami. Zaokrouhlejte na 3 desetinná místa.
Děkuji za každou pomoc!
Offline
- (téma jako vyřešené označil(a) gadgetka)
#2 16. 06. 2015 20:30
Re: Geometrie
↑ anicka3112:
Zdravím,
těžnice ta spojuje vrchol A a střed strany BC, který označím A1. Trojúhelník CAA1 je pravoúhlý, známe v něm dvě délky. Třetí je jeho odvěsnou a zároveň polovinou strany BC. Užij Pythagorovu větu.
Offline
#3 16. 06. 2015 20:36
- anicka3112

- Zelenáč
- Příspěvky: 9
- Reputace: 0
Re: Geometrie
↑ Al1: výsledek je tedy = 5,1807 a pro ziskani normalni strany a tedy odvěsny to vynásobím 2? takže to bude =10.3614?
Offline
#4 16. 06. 2015 20:45
Re: Geometrie
↑ anicka3112:
Ano, jen zaokrouhluj na tři desetinná místa. A pro obsah rovnostranného trojúhelníku můžeš užít vztah 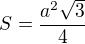
Offline
#5 16. 06. 2015 20:49
- anicka3112

- Zelenáč
- Příspěvky: 9
- Reputace: 0
Re: Geometrie
↑ Al1: děkuji už mi vyšel výsledek. že obsah S1=57,309, a S2=46,484, S3=10,825. Je to správně prosím?
Offline
#7 16. 06. 2015 20:54 — Editoval Al1 (16. 06. 2015 20:54)
#10 17. 06. 2015 11:23
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Geometrie
Zdravím,
jen drobnost k zadání:
Výpočtem dokažte, že obsah rovnostranného trojuhelníku sestrojeného nad přeponou, se rovná součtu obsahů rovnostranných trojuhelníků sestrojenými nad oběma odvěsnami. Zaokrouhlejte na 3 desetinná místa.
to samozřejmě nejde - výpočtem, navíc zaokrouhleným, se nic nedokazuje.
Toto znění: "obsah rovnostranného trojuhelníku sestrojeného nad přeponou, se rovná součtu obsahů rovnostranných trojuhelníků sestrojenými nad oběma odvěsnami" je zápisem (po úpravě) Pythagorovy věty (pokud je považována za dokázanou, tak vztah obsahů bude také platit). Úloha snad mohla být jako "pro věličiny zadané v úloze odvoďte vztah pro výpočet obsahu rovnostranného trojúhelníku sestrojeného nad přeponou (odvěsnou))" (nebo něco podobného).
↑ anicka3112: odkud je úloha? Děkuji.
Offline
#11 18. 06. 2015 11:45 — Editoval vanok (18. 06. 2015 11:46)
Re: Geometrie
↑ jelena:
Pozdravujem, tvoja didakticka poznamka by mala zaujat vyucujucich. Taka chyba, zial, moze odradit vela talentov od matematiky.
Ako si poznamenala, ide o malu generalizaciu Pythagora, platnu pre vsetky pravidelne mnohouholniky.... Je to dobra tema pre mat. kruzok na zakladnej skole ( iste take existuju).
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
