Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 18. 06. 2015 09:10 — Editoval Meglun (18. 06. 2015 09:11)
Exponenciální nerovnice
Ahoj. Včera jsem psal test, kde bylo daní o nalezení všech možných řešení pro x. A já vůbec nevím jak s touto rovnicí naložit.
příklad je zde: wolframalpha
Společnost tě může připravit o všechno, ale to co máš v hlavě, ti nikdo neveme.
Offline
- (téma jako vyřešené označil(a) Meglun)


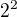 a
a  ?
?