Matematické Fórum

Blackflower · 17. 06. 2015 22:19

Ahojte,
mám jeden nekonečný rad a teda aj jeho súčet:
$\sum_{n=0}^{\infty} \frac{(n+2)(n+3)}{3^n} = \frac{57}{4}$
Nemá niekto náhodou nápad, ako sa k tomu súčtu dostať?
Vopred vďaka za každú radu.

jarrro · 18. 06. 2015 09:44 — Editoval jarrro (18. 06. 2015 09:47)

$\sum_{n=0}^{\infty} {(n+2)(n+3)x^n}=\frac{$ \sum\limits_{n=0}^{\infty} x^{n+3}$^{\prime\prime} }{x}$

vanok · 18. 06. 2015 09:59 — Editoval vanok (18. 06. 2015 10:28)

Ahoj ↑ Blackflower:,
Pochpitelne na vysetrenie tvojho radu treba najprv ukazat ze konverguje.

Mozna metoda je pouzitie funkcie $f_n(x)=\sum_{k=0}^{n}x^n$
( ktora je definovana ako rada).
Vysetrit jej prvu a druhu derivaciu, ich vyjadrit v bode 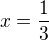$x=\frac13$ , a aj ich limity v nekonecne... A vdaka tomu vyjadrit hladanu limitu.

Blackflower · 18. 06. 2015 10:27

↑ vanok: Vďaka za reakciu. Aby som objasnila situáciu, tento príklad nie je pre mňa, ale zaoberá sa ním moja mama, ktorá sa tiež venuje matematike. :) Konvergenciu radu sa jej podarilo dokázať, pýtala sa ma, či neviem, ako sa dopátrať k súčtu, keď my sme brali v škole nejaké finty... ale žiaľ si ich už moc nepamätám.

vanok · 18. 06. 2015 10:33

↑ Blackflower:
Ale aj co napisal kolega ↑ jarrro: je dobre.
Ale ak treba dokaz, tak myslienka metody, co som napisal vyssie sa da pouzit.

Blackflower · 18. 06. 2015 10:35

↑ vanok: Ja som si aj myslela, že tam bude niečo takéto, ale toto mi nenapadlo. ↑ jarrro: je proste pán. :)
Či treba dôkaz, to neviem, ale môže sa to zísť. Vďaka. :)

vanok · 18. 06. 2015 11:34

↑ Blackflower:
A nevahaj pozriet aj na cvicenia math.stackexchange.com ako napr. tu
http://math.stackexchange.com/questions … 0n-frac14n
Casto su tam poucne temy.

Matematické Fórum

#1 17. 06. 2015 22:19

Nekonečný rad

#2 18. 06. 2015 09:44 — Editoval jarrro (18. 06. 2015 09:47)

Re: Nekonečný rad

#3 18. 06. 2015 09:59 — Editoval vanok (18. 06. 2015 10:28)

Re: Nekonečný rad

#4 18. 06. 2015 10:27

Re: Nekonečný rad

#5 18. 06. 2015 10:33

Re: Nekonečný rad

#6 18. 06. 2015 10:35

Re: Nekonečný rad

#7 18. 06. 2015 11:34

Re: Nekonečný rad

Zápatí