Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Kvadratická Forma V4 (TOTO TÉMA JE VYŘEŠENÉ)
#3 29. 06. 2015 15:48 Příspěvek uživatele Bores byl skryt uživatelem Bores. Důvod: špatný příspěvek.
#4 29. 06. 2015 16:17 Příspěvek uživatele Bores byl skryt uživatelem Bores.
#5 29. 06. 2015 16:20 Příspěvek uživatele Bores byl skryt uživatelem Bores. Důvod: chybný obrázek
#7 29. 06. 2015 17:55
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Kvadratická Forma V4
↑ Bores:
děkuji, dolní indexy jsou pomoci zápisu x_1:  . Zde je materiál od vás (nebo přidej, prosím, své materiály). Umíš sestavit matici zadané kv. formy a použit na ověření Sylvestrovo kriterium (zatím jsem nekontrolovala, zda bude fungovat na Tvé zadaní), nebo používáš jinou techniku? Děkuji.
. Zde je materiál od vás (nebo přidej, prosím, své materiály). Umíš sestavit matici zadané kv. formy a použit na ověření Sylvestrovo kriterium (zatím jsem nekontrolovala, zda bude fungovat na Tvé zadaní), nebo používáš jinou techniku? Děkuji.
Offline
#9 29. 06. 2015 18:13
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Kvadratická Forma V4
↑ Bores:
matice 4x4 a na zbytku pozic jsou 0 - souhlasí? Tak, jak máš, budeš používat subdeterminanty (hlavní - tedy z levého horního rohu). Pokud až do 3x3 problém není, tak poslední 4x4 můžeš Laplace rozvoj podle některého řádku nebo sloupce, nebo jinou techniku, kterou umíš).
Offline
#11 29. 06. 2015 18:47
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Kvadratická Forma V4
↑ Bores:
číselný výsledek budu považovat za platný (případně překontroluj ve WA), podle Sylvestr. kritéria by byla pozitivně semidefinitní (máte stejnou metodu a definici?). Jiný možný postup je přes vlastní čísla.
a výsledek má být že že je indedinitní
to je výsledek k úloze ze sbírky? nebo Tvůj závěr, který se nezdá?
Offline
#12 29. 06. 2015 18:53
Re: Kvadratická Forma V4
Nepovažujte ho za platný protože není, neb tohle přeci není Indefinitní, výsledek je ze sbírky. Abych to to popsal takže dělám
(0 0 0 -2) D1 = 0? Protože podle toho pravidla mě zajímá levý horní roh = 0
(0 0 -1 0) D2 = 0? protože v levém horním rohu jsou všude nuly takže také = 0
(0 -1 0 0) D3 = 0? protože také tam nemůžu nic dělat
(-2 0 0 0) D4 = ?? ted mam rozvíjet řádkem a výsledek toho je determinant č 4 nebo jak? jsem velice zmaten.
Offline
#13 29. 06. 2015 19:02
Re: Kvadratická Forma V4
Ahoj ↑ Bores:,
Mozes tiez pouzit, ze
Ako aj podobnu relaciu pre  a potom vyuzit zname vety...
a potom vyuzit zname vety...
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#15 29. 06. 2015 19:31
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Kvadratická Forma V4
↑ vanok:
Zdravím a děkuji za další postup. Je to varianta úpravy na čtverec? Děkuji.
↑ Bores: zkusíme dodělat metodu Sylvestrova kriteria - vychází mi to stejně a také mám, že "indefinitní" bych neurčila (mám "pozitivně semidefinitní"). Je možné, že neurčujete "semidefinitní"? Přidej, prosím, vaši teorii. Případně zkusíme další úlohu ze sbírky - nebo narazil jsi na další s neshodným výsledkem?
Metodu vlastních čísel také používáte? Až dořešíme Sylv. K., tak ještě prosím pokračuj s kolegou ↑ vanok:, pokud jste metodu také zaváděli.
Offline
#16 29. 06. 2015 19:40
Re: Kvadratická Forma V4
O metodě vlastních čísel slyším poprvé. 
Tady je sbírka od našeho profesora ze které to mám. Ostatní příklady jsem nějaké zkoušel a vyšlo mi to.
Nicméně řeším hlavně tento, protože obdobný jsem dostal minulý týden ve zkoušce a nevěděl jsem co s ním, tak abych na příští věděl.
Offline
#18 29. 06. 2015 20:00
Re: Kvadratická Forma V4
↑ jelena:
Pozdravujem,
Ano to je Gauss-ova metoda.
Sylvestrova veta umoznuje rychlo upresnit potom typ kvadratickej formy.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#19 29. 06. 2015 20:14
#21 30. 06. 2015 10:17
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Kvadratická Forma V4
↑ Bores: děkuji za zprávu, označím za vyřešené.
O metodě vlastních čísel slyším poprvé.
to se dá případně dohledat (okolo kvadratických forem), jsou to další metody na ověření + viz kolega ↑ vanok:. Pokud jste brali Sylvestrovo kritérium a úlohy jsou tak i postaveny, že jde použit, tak v pořádku, že máš nacvičeno (pravděpodobně se předpokládá jeho použití i v úlohách na extrémy funkcí více proměnných). Zdárnou zkoušku přeji.
Offline
#23 22. 01. 2019 15:42 — Editoval ježek (22. 01. 2019 15:45)
Re: Kvadratická Forma V4
jelena napsal(a):
↑ vanok:
↑ Bores: zkusíme dodělat metodu Sylvestrova kriteria - vychází mi to stejně a také mám, že "indefinitní" bych neurčila (mám "pozitivně semidefinitní"). Je možné, že neurčujete "semidefinitní"? Přidej, prosím, vaši teorii. Případně zkusíme další úlohu ze sbírky - nebo narazil jsi na další s neshodným výsledkem?
Vlastní čísla matice kvadratické formy v posledním příkladu jsou -2, 2, -1, 1. Aby byla pozitivně semidefinitní, tak by její vlastní čísla musela být nezáporná. Tato kvadratická forma je tedy indefinitní.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Kvadratická Forma V4 (TOTO TÉMA JE VYŘEŠENÉ)

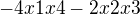 a mám určit typ kvadratické formy.
a mám určit typ kvadratické formy. různý od
různý od  je kvadratická forma negativně definitní.
je kvadratická forma negativně definitní.