Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 06. 07. 2015 12:20
Kombinatorika
zdravím
Zde mám tři příklady a nevím, jak na ně
1) Kolik nejvýše čtyřmístných čísel lze sestavit z číslic 1 až 6, když se žádné neopakuje
2)Kolika způsoby se může 5 žen a 2 muži posadit v kině na určených 7 sedadel
3) Kolik sudých přirozených čísel <300 000 lze vytvořit z číslic 1 až 5
děkuju
Offline
- (téma jako vyřešené označil(a) Simon52)
#2 06. 07. 2015 13:02 — Editoval Al1 (06. 07. 2015 13:04)
Re: Kombinatorika
↑ Simon52:
Zdravím,
ad1 - pravidlo součinu a součtu
nejvýše čtyřciferná znamená jedno nebo dvoj nebo tří nebo čtyřciferná čísla
první místo v čtyřciferném čísle lze obsadit jednou ze 6 číslic, druhé už jenom některou z 5, třetí ze 4 a poslední ze 3 číslic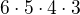
Podobně i pro zbývající jedno nebo dvoj nebo tříciferná čísla. Nakonec všechny určené počty sečteš.
Offline
#5 06. 07. 2015 20:58
- xstudentíkx
- Příspěvky: 962
- Škola: VŠE
- Pozice: student
- Reputace: 26
Re: Kombinatorika
Ahoj ↑ krauva:
Co se druhého příkladu týče, tak dle mého se jedná o klasickou permutaci a výsledek je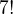 
.
Na první vybírám ze 7 lidí, na druhé z 6, na třetí z 5, atd.
Offline
#6 06. 07. 2015 21:05 — Editoval Al1 (06. 07. 2015 21:06)
Re: Kombinatorika
↑ Simon52:
ad 2)
Pokud nemáme žádné podmínky pro posazení těchto sedmi osob, pak počet jejich usazení odpovídá číslu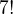, neboť první sedadlo obsadíme některým ze sedmi osob, na druhé už máme výběr jen ze šesti osob atd. (jedná se o permutace bez opakování)
ad3)
Hledáš čísla sudá a
jednociferná .... počet určíš snadno
dvojciferná ... první místo obsadíš pěti způsoby, druhé jen dvěma, neboť aby bylo číslo sudé, musí končit na sudou číslici, počet ...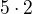
stejně určíš všechna troj, čtyř a pěticiferná čísla,
šesticiferná musí začínat na 1 nebo 2 (aby byla menší než 300 000) a opět končí na 2 nebo 4.
A teď jednotlivé počty sečti a máš výsledek.
Offline