Matematické Fórum

↑ rss:Ahoj, najprv by som si chcel vybrať bod v ktorom rozviniem Taylora, lebo v štartovom bode mi vychádzali nekonečná.( alebo som sa pomýlil...neverím síce okrajovým bodom, hoci sú lákavé, keď potom vyjdú nuly)

Tak som to nakreslil pre dva hmotné body vzdialené 0.2 metra.

No a sleduj prosím ako sa približujú...
Ich vzdialenosť sa samozrejme zmenšuje, čas vzrastá až sa dosiahne určité maximum.

No ale body sú nie ešte stále pri sebe !!!!

Sú vo vzdialenosti akýchsi 0.05m.

A rýchlost vzájomná je nekonečná...
==========================================
Tak tieto poznatky ma rozladili, že nemám zatiaľ náladu rozvíjať Taylora. :-(
Však sa to vracia v čase ....

↑ pietro:
↑ rss:

1. Zde uvedené řešení je správně, neni důvod proč by být nemělo
2. Graf ti vyšel tak divně proto, že si omylem protáhl odmocninu i přes Arccos
3. r pomocí elementárních funkcí a konečného počtu operací vyjádřit nelze, nicméně není to problém, neboť software si s tím lehce poradí. To není na škodu, neboť i hodnoty elementárních funkcí nám vyčísluje software.



4. V podstatě už nejsem středoškolák
5. Ve svém tématu se bav o čem chceš, mazat ti to nebudu, je to tvoje téma. Mažu jen takové příspěvky, ve kterých svoje bláboly šíříš do cizích témat, popřípadě urážíš ostatní. Toho jsi si už mohl všimnout.
6. Apjar toho píše spoustu, nespočítal však zatím nic.
7. Pokud chceš nad výsledkem dál polemizovat (i když nevím, co chceš ještě řešit) tak budiž. Pokud ne, označ prosím téma jako vyřešené

Toť ode mne vše
Hezký den

↑ rss: Ahoj, myslím, že ešte nenastala doba, keď za svoje názory sa musíme stiahnuť do ilegality.

A boli v minulosti aj také obdobia...

Vnímam túto snahu o zachovanie "čistoty".

Podľa mňa je to ako keď niekto na školskú nástenku dopíše 1+1=3.

(To sa predsa nesmie.) Vidí to školopovinná mládež a ako to bude vplývať na jej ďalší vývoj....
==========================================
To nevadí ?, že z internetovej oblasti sa tlačí na dieťa zával iného vadného materiálu..

ale nič, ideme počítať inverznú...:-) ku t(r).

↑ rss:Ahoj, jedno z možných zoskupení premenných a operácií

Taylorovým rozvojom za použitia inverzných derivácií

..nevýhoda...pre vysoké k sa stroje preťažia vo svojich rozsahoch.

A preto aproximácia nie je presná :-(

K diskutované analýze řešení...

Může být na zamyšlení, co je vlastně "řešení ve správném tvaru". Většinou se tvar výsledku, který lze vyčíslit s vlastností superkonvergence (tedy že chyba klesá exponenciálně s počtem iterací), dá považovat za finále. Neboť výpočet takové odmocniny se počítá stejně rychle (například půlením intervalů).

Taylorovy rozvoje mají jeden všeobecný neduh. Pokud se ptáme na přesnost hodnoty v pevném bodě, tak s přikládáním vyšších a vyšších členů Taylorova rozvoje chyba sice klesá exponenciálně. Nicméně když si otázku položíme tak, jak intenzivně se rozšiřuje oblast, kde řešení známe řekněme s přesností 1%, tak tato oblast roste s přikládáním vyšších řádů velmi pomalu. Na malých vzdálenostech od bodu, kde vyjadřujeme rovnost, tak můžeme získat věrné řešení, ale dříve nebo později (spíš dříve) nám Taylorova řada libovolného řádu bude značně od řešení divergovat. Využiji obrázek z wikipdie, který demonstruje, jak dobře se blíží vyšší řády Taylorova rozvoje k funkci sinus:



Je dobré se nebát tolik speciálních funkcí (například eliptické integrály) nebo řešení, které jsou prezentovány jako inverzní funkce. Ruku na srdce, umíte opravdu počítat obyčejnou odmocninu? :). Jestli ano, pak pro vás vůbec není překážka se vypořádat s inverzní funkcí nebo jinou konstrukcí. Jediné, co hraje do karet odmocnině je to, že se to jen objevuje často a proto to lidi implementovali do kalkulaček přednostně. Ostatně, třeba hledáček řešení kubických rovnic už je v řadě kalkulaček implementováno také.

Pokud hledáme řešení ve tvaru nějakých polynomů, bývá mnnohem lepší používat speciálnější polynomy, například kubický spline (což je vlastně úlně obyčejný polynom třetího řádu). Které nejsou odvozeny pouze od hodnot derivací v jednom bodě, ale snaží se aproximovat řešení na určitém intervalu na základě hodnot derivací na obou koncích intervalu. Tyto aproximace mají zpravidla mnohem lepší vlastnosti.

Ještě si dovolím další formulaci řešení (v podstatě je to jen přehazování konstant a algebraická úprava rovnice)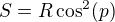





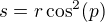
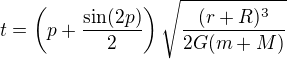
Je to jen zkrátka parametrické vyjádření řešení. Na levé straně je vždy hodnota, kterou hledáme (S,s,t) a na pravé straně jsou konstanty pohybu (r,R - počáteční hodnoty, G,M,m - fyzikální konstanty) a parametr p. Různé hodnoty parametru p pak jen vykreslují jednotlivé body řešení. Hodnoty parametru p v intervalu 0..pi/2 nám tak vykreslí všechny body trajektorie pádu. Pokud bychom rádi vykreslili trajektorii, tak tady máme zcela exaktní metodu, jak kreslit jednotlivé body. Jediný problém je jen to, že zadáváme apriori hodnotu p a nevíme dopředu, pro jaký čas počítáme bod trajektorie. Nicméně metodou půlení intervalu to můžeme snadno nalézt - tedy metodou, která je srovnatelná s tím, jak se počítá i obyčejná odmocnina.

Doporučuji položit si otázku, jak se vlastně počítá odmocnina nebo hodnota funkce sinus :). Pokud tušíte, pak by vám řešení v podobně implicitním tvaru neměla vůbec překážet. Respektive o nic víc, než řešenní ve tvaru goniometrické funkce. Balíček elementárních funkcí je prostě jen hromádka předem nadefinovaných funkcí, které se jen vyskytují častěji. Řešení v jejich tvaru není o nic hodnotnější. Neměli bychom lámmat hůl nad řešením, o kterém se zkrátka jen lidé nedohodli, že pro tento tvar nevymysleli značku podobnou klikiháku v odmocnině.

A ešte sa mi s prepáčením tvoria otázky...:

1. ako by sme mohli skontrolovať analytický výsledok spätným dosadením do východiskovej diferenciálnej rovnice
trebárs podľa http://homen.vsb.cz/~kre40/esfmat2/kapi … la_5_3.pdf



2. predstavme si, že máme k dispozícii len hodnoty r v závislosti na čase v tvare dátového súboru... od r=R v t=0 do r=0 v čase t=inf.
Vedeli by sme z nameraných údajov zostaviť
Newtonov gravitačný zákon? Teda spätne zrekonštruovať z nameraných hodnôt exaktný analytický predpis?

3. Ako by sa daná úloha dala riešiť pomocou zakriveného časopriestoru?

↑ pietro: ↑ Brzls: ↑ rughar: Ďakujem, asi ste vyriešili problém. S t a č í   m i   z á v i s l o s ť   č a s u   n a   v z d i a l e n o s t i . Potrebujem vytvoriť OpenOffice tabuľku, kde budú časy a vzdialenosti, a z nej niečo vypočítam. Stačií mi zopár variant: zmena počiatočnej vzdialenosti povedzme na 1/2 alebo 1/3, dve porovnateľné hmotnosti, a dve značne rozdielne hmotnosti.

Pre istotu sa ešte raz spýtam, či je toto správny vzorec:


↑ rughar: Čo sa týka "vyžarovania gravitačných vĺn",tak to by sme si mali ujasniť pojem "žiarenie". Pole môže konať prácu spojito s akoukoľvek malou alebo veľkou energiou, alebo nespojito pomocou kvánt, kde už nie je silové pôsobenie a existuje minimálna energia prenášaná kvantom. Meranie akožegravitačných vĺn bolo robené na základe pôsobenia sily, malých energií, a sama gravitácia nemôže vytvoriť žiarenie rovnako ako elektrická intenzita.

↑ rss:

Kvantová podstata gravitačního záření není známá. Gravitační záření není ani pořádně pozorované, takže analogie k Planckově kvantové hypotéze ke gravitaci neexistuje. Uvažuje se, že by analogicky k fotonu existoval graviton, nicméně neexistuje zatím žádně pozorování takového kvanta.

"Záření", které jsem měl na mysli, jsou gravitační vlny podle Obecné teorie relativity. Asi tak, jako Maxwellovy rovnice předvídají elektromagnetické vlny bez další znalosti fotonů, tak OTR umí předpovědět gravitační vlny. Není důvod si myslet, že by to mělo být špatně. Elektromagnetické vlny popsané Maxwellovýmy rovnicemi bez kvantové hypotézy docela věrně popisují většinu známého elektromagnetického záření (rádiové vlny, kosmické záření, ...). Prvním krokem je uvažování klasických nekvantových vln. To, že médiem pro šíření vlny je nějaká součást standardního modelu jako je foton (elektromagnetismus) nebo graviton (hypotetická pro gravitaci) je snaha posunout přesnost o další řád.

Nekvantové pojetí gravitačních vln je jen "mezikrok" k přesnějšímu vyjádření. To je ale přísně vzato úplně jakýkoliv popis a zřejmě i ten kvantový.

↑ rss: Ahoj, posielam testovanie analytického riešenia

↑ misaH: To ja nie..to rughar  a potom  ...ďaleko ďaleko stroj.

Len neviem,  prečo Newtona ako prvé napadlo, že sila je nepriamo úmerná

štvorcu vzdialenosti, keď aj to čudo vľavo má rovnaké hodnoty... :-)