Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 04. 08. 2015 04:25 — Editoval vanok (04. 08. 2015 07:06)
Re: teória čísel
Ahoj ↑ vytautas:,
Toto cvicenie sa da riesit aj stredoskolskymi metodamy.
Napr. vysetrit nejaku vlastnost mod 65, staci vybrat po jednom vsetkych moznych representantov. To sa urobi napriklad vyberom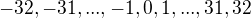 . Vyhoda tohto vyberu pre tvoje cvicenie je zrejma.
. Vyhoda tohto vyberu pre tvoje cvicenie je zrejma.
Teraz mozes uvazovavat o stvorcov vsetkych tychto representatov, a konstatovat, ze modulo 65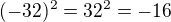

...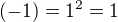
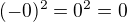
To ti umozni po vypoctoch konkretneho vycislenia kazdeho riadku aj tie z .... (ktore pochopitelne pre jasnost musia byt napisane ako representanty modulo 65 vybrane vyssie) dat odpoved na otazku tvojho cvicenia.
Tak po vypoctoch a uvahach, budes mat dokonale riesenie....
Urob to podrobne, potom mozme hladat ine moznosti dokazu....
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 04. 08. 2015 06:29 — Editoval vanok (04. 08. 2015 09:58)
Re: teória čísel
Pridam ti tu este malu poznamku. Ako postupovat ak by si chcel riesit take rovnice ( ak je to mozme)
Ukazem ti to na jednom priklade.
Riesenie rovnice 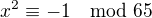
Ktora sa ekvivalentne pise 
ma riesenia  (Medzi representatmy co som napisal vyssie)
(Medzi representatmy co som napisal vyssie)
To jednoducho uvidis z vypoctov o ktorych som pisal v ↑ vanok:.
Tiez mozes konstatovat, ze 
co su 2 mozna faktorizacie ( v pripade ak by sa pracovalo modulo p, prvocislo je mozne len jedina faktorizacia)
Poznamka.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 04. 08. 2015 16:11 — Editoval vytautas (04. 08. 2015 16:18)
Re: teória čísel
↑ vanok:
ďakujem za vyčerpávajúci príspevok
mám pár otázok naň:
v prvom rade, je mi jasné, že zvyšky po delení 65 môžu byť len  ale prečo ma zaujímajú ich mocniny ? však v tej rovnici je zvyšok n a číslo x môže byť ľubovoľné, nie ?
ale prečo ma zaujímajú ich mocniny ? však v tej rovnici je zvyšok n a číslo x môže byť ľubovoľné, nie ?
uniká mi pointa
vopred ďakujem za ochotu a čas.
edit : práve som pochopil, tie čísla, tento príspevok teda ignorujte, ďakujem.
Per aspera ad astra
Offline
#5 04. 08. 2015 16:37
Re: teória čísel
↑ vanok:
keď som si prešiel všetky "representanty" tak každý má dvojicu s opačným znamienkom, takže to platí.
aká je teda iná možnosť riešenia ? hlavne elegantnejšia
čo sa týka poznámky, zvykol som si tieto čísla značiť 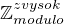 no vidím, že váš zápis je jednoduchší.
no vidím, že váš zápis je jednoduchší.
ešte jedna otázka, z čoho vyplýva, že  ? vidím, že to platí, no chcel by som vedieť prečo.
? vidím, že to platí, no chcel by som vedieť prečo.
ďakujem .
Per aspera ad astra
Offline
#6 04. 08. 2015 17:13
Re: teória čísel
↑ vytautas:,
Pri beznom deleni cislom 65 sa uvazuju zvysky 
Tu som ti navrhol miesto klasickych zvyskov pouzitie ich representantov tak aby si mal bez tazkosti "kladne ako aj zaporne representacie" ako napr v tvojom prvom prispevku.
Tie mocniny nas zaujimaju lebo chces vysetrovat rovnice ako 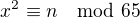 . A tak je zaujimave vediet ako su mozne obrazy pre funkciu
. A tak je zaujimave vediet ako su mozne obrazy pre funkciu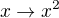 modulo 65. Lebo je jasne ze len pre n ktore su v obraze moze mat rovnica typu
modulo 65. Lebo je jasne ze len pre n ktore su v obraze moze mat rovnica typu 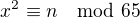 aspon jedno riesenie.
aspon jedno riesenie.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 04. 08. 2015 17:38 — Editoval vanok (04. 08. 2015 19:29)
Re: teória čísel
Ilustraciu  dostanes vdaka tabulke co som ti navrhol urobit.Jeden z riadkov z nej je
dostanes vdaka tabulke co som ti navrhol urobit.Jeden z riadkov z nej je  a iny
a iny 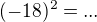 ( je to uzitocna etapa na hladanie rieseni a tiez ked je uz cela urobena umozni ti to bez omylu dat odpoved na danu otazku cvicenia) potom identita
( je to uzitocna etapa na hladanie rieseni a tiez ked je uz cela urobena umozni ti to bez omylu dat odpoved na danu otazku cvicenia) potom identita 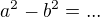 mod 65 pochopitelne plati....
mod 65 pochopitelne plati....
No ale tu nas zaujimaju vysledky modulo 65, tak to nemozes pouzit v opacnom smere, cize povedat co plati mod 65, plati aj v prirodzenych ciskach.( priklad, mod 65 mas  ale to pochopitelne neplati pre celé cisla... To je jedna z pricin, preco sa taketo teorie neucia na SS)
ale to pochopitelne neplati pre celé cisla... To je jedna z pricin, preco sa taketo teorie neucia na SS)
Chcel by som vidiet ze vdaka tabulke si schopny napisat dobry dokaz ... Tak ho nam tu podrobne napis.( vediet pisat zrozumitelne riesenie je nevyhnutne, ak chces napredovat)
Tato technika riesenia je "vysetrenie vsetkych moznych pripadov ( alternativ)".
Aky je zdroj tvojho cvicenia?
Nemozem ti tu navrhovat ine riesenia, ben toho aby som vedel co si uz nastudoval a pochopil.
Take zakladne citanie mas napr tu
http://mathafou.free.fr/themes_en/kcongr.html
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 04. 08. 2015 20:17 — Editoval vytautas (04. 08. 2015 20:20)
Re: teória čísel
↑ vanok:
ak som to správne pochopil, tak 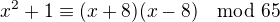
pretože platí  a
a 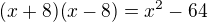
čo sa dá zapísať ako  alebo
alebo 
hmm, čo sa týka dôkazu, nejaký náčrt
keďže pracujeme mod 65, tak stačí uvažovať čísla (-32,-31 ,, 0 ,, 31 ,32) pretože každé iné číslo je kongruentné s nejakým číslom z tejto množiny.
po vypísaní tabuľký všetkých druhých mocnín čísel z množiny je vidieť, že každý zvyšok sa objavuje vždy aj s jeho opačným číslom .
čiže rovnica 
ako urobiť korektný dôkaz mi nenapadá.
zdroj: Birkhoff,Saunders Prehľad modernej algebry
pred touto kapitolou sú komutatívne okruhy, obory integrity, euklidov algoritmus, základná veta aritmetiky, dobré usporiadanie.
toto by som mal ako tak zvládať.
ďakujem za ochotu
odkaz prezriem, vyzerá byť dosť užitočný, no chýbajú mi dôkazy tvrdení.
Per aspera ad astra
Offline
#9 04. 08. 2015 21:47 — Editoval vanok (04. 08. 2015 21:54)
Re: teória čísel
To na zaciatku si priliz komplikujes.
Staci povedat
Vseobecne pre kazde celé cislo plati 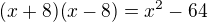
Toto sa pise modulo 65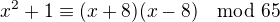 .kOniec dokazu.
.kOniec dokazu.
Poznamka
Toto ( tvoj druhy riadok)  nema zmysel.
nema zmysel.
Tvoj riadok 3, to je len ukazka ze 
da  .... A vtedy nas moze napadnut ta faktorizacia.
.... A vtedy nas moze napadnut ta faktorizacia.
Tvoj nacrt dokazu je celkom dobry. ( napisat tu celu tabulku by to este viac objasnilo)
To si chcel napisat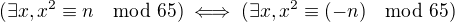
Takyto dokaz sa casto pouziva (povie sa tiez ze je konstruktivny).
Ked hovoris o mnozine, tak pis 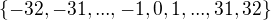 . To tvoje znacenie z (...) znamena postupnost alebo aj 65-ticu.
. To tvoje znacenie z (...) znamena postupnost alebo aj 65-ticu.
Bolo by dobre (a elegantne) napisat aky je skutocne obraz 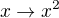 I ked sa da vycitat z tes tabulky. A povedat, ze ze len pre prvky obrazu rovnica
I ked sa da vycitat z tes tabulky. A povedat, ze ze len pre prvky obrazu rovnica 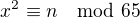 moze mat riesenie.
moze mat riesenie.
Na koniec citanie co som ti postal vyssie dava klucove myslienky dokazov. A riesenie cvicenia mozu ti velmi posluzit. Tiez tam poklikaj aj na ine temy...
Kniha co citas, je vyborna.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#10 04. 08. 2015 22:12
Re: teória čísel
↑ vanok:
tabuľka:
"Bolo by dobre (a elegantne) napisat aky je skutocne obraz
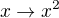 I ked sa da vycitat z tes tabulky. A povedat, ze ze len pre prvky obrazu rovnica
I ked sa da vycitat z tes tabulky. A povedat, ze ze len pre prvky obrazu rovnica 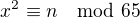 moze mat riesenie."
moze mat riesenie."nechápem presne túto vetu. v akom zmysle "aký" má byť obraz ?
myslí sa tým injekcia/surjekcia/bijekcia ?
ďakujem .
Per aspera ad astra
Offline
#11 04. 08. 2015 22:56
Re: teória čísel
Obraz je vytvoreny vsetkymi prvkamy co su na pravo rovnosti. Napr tam nie je 3.
Tak 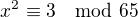 nema ziadne riesenie.
nema ziadne riesenie.
Obraz 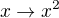 mod 65 je
mod 65 je 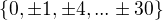
To uz lahucko doplnis z tej tabulky.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#13 04. 08. 2015 23:17
Re: teória čísel
↑ vytautas:,
Pochopitelne, tu pracujes modulo 65=5x13.
Keby sa pracovalo z nejakym prvocislom, situacia by bola v nieco mais jednoduchsia ...
Ale take prehlbenia si nechaj na druhe citanie tvojej knihy.
Tu je dolezite pochopit ako sa pracuje v okruhoch a potom v telesach.
Napreduj v tvojom citani a skus takto ako v tomto cviceni analyzovat situacie.
Dobre pokracovanie.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#14 05. 08. 2015 20:54
Re: teória čísel
no ked uz si odpozoroval nejake zakonitosti, tak aby si urobil nejaky elegantny dokaz tak by si mohol postupovat takto:(vsetko bude mod 65)
predpokladas, ze 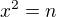 ma riesenie a hladas riesenie rovnice
ma riesenie a hladas riesenie rovnice  . dokazes napisat taku funkciu (presny predpis)
. dokazes napisat taku funkciu (presny predpis) 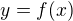 ktora bude splnat
ktora bude splnat  ?
?
hint: najpv by som skusal linearne fcie :) a odpoved uz mas v predchadzajucich prispevkoch.
Offline
#15 06. 08. 2015 01:15
Re: teória čísel
Ahoj ↑ Brano:,
To myslis o vyuzitie 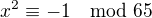 jedneho z rieseni ktore som popisal tu ↑ vanok: ?
jedneho z rieseni ktore som popisal tu ↑ vanok: ?
Pochopitelne je to mozna cesta, i ked neviem ci to treba povazovat za "elegantny dokaz", ja by som len povedal iny dokaz.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#17 06. 08. 2015 13:12 — Editoval vanok (06. 08. 2015 18:43)
Re: teória čísel
↑ Brano:,
To je pravda, a iste si poznamenal, prave preto som napisal vyssie riesenia 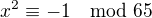 . No vsak myslenie pomocou " morfismov" nie je asi uplne prirodzene, i ked by som ho cakal od vysokoskolaka po studiu prveho rocniku VS. No vsak tu kolega zatial precital len zaciatok peknej Birkhoff-vej knihy. Iste po jej precitani a vyrieseni cviceni bude pouzivat co najucinejsie metody riesenia.
. No vsak myslenie pomocou " morfismov" nie je asi uplne prirodzene, i ked by som ho cakal od vysokoskolaka po studiu prveho rocniku VS. No vsak tu kolega zatial precital len zaciatok peknej Birkhoff-vej knihy. Iste po jej precitani a vyrieseni cviceni bude pouzivat co najucinejsie metody riesenia.
Akoze kolega nereagoval pridavam jednu variantu toho kratkeho dokazu, ktory si moze pozriet pre kontrolu.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline

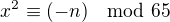 má riešenie.
má riešenie. su cisla, ktore su vsetki ekvivalentne modulo
su cisla, ktore su vsetki ekvivalentne modulo 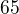 . Zapis, ako
. Zapis, ako ![kopírovat do textarea $[-1]_{65}$](/mathtex/ad/ad54f1beb51d9f2915d1e797b1f1ef09.gif) kde miesto
kde miesto  moze byt lubovolny iny representant zoznamu, moze byt uzitocny ak chces prehlbit teoriu (pochopitelne v nejakej knihe mozes najst ine oznacenia ....) . Take oznacenia umoznuju tiez pisat kratcie niektore vyrazy ....a tiez uviest pojmy okruhu, telesa.
moze byt lubovolny iny representant zoznamu, moze byt uzitocny ak chces prehlbit teoriu (pochopitelne v nejakej knihe mozes najst ine oznacenia ....) . Take oznacenia umoznuju tiez pisat kratcie niektore vyrazy ....a tiez uviest pojmy okruhu, telesa. 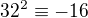
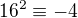
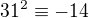
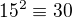
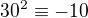
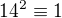


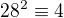
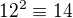

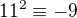
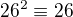
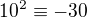

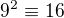
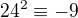
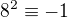
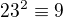
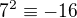


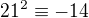
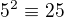
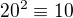


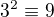
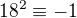

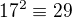
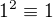
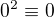
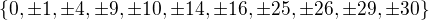
 ma aspon jedno riesenie
ma aspon jedno riesenie  .
. , tak tiez
, tak tiez  .
.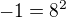 ( vybrali sme aleatorne jedno zo 4-och rieseni
( vybrali sme aleatorne jedno zo 4-och rieseni  , co znamena ze rovnica
, co znamena ze rovnica 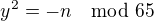 ma riesenie. ( tu ide o
ma riesenie. ( tu ide o  ). To sa vyjadri takto: Ak
). To sa vyjadri takto: Ak