Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 16. 08. 2015 12:48
delitele jednotky
zdravím
mám úlohu : "Ukážte, že prvok 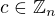 , ktorý nie je deliteľom jednotky, je deliteľom nuly.
, ktorý nie je deliteľom jednotky, je deliteľom nuly.
moje riešenie.
ak je prvok deliteľom jednotky v 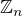 tak existuje riešenie rovnice
tak existuje riešenie rovnice  , čiže
, čiže 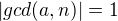
keď prvok nie je deliteľom jednotky, tak  a to znamená, že je deliteľom nuly v
a to znamená, že je deliteľom nuly v 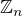 .
.
je to správne ?
ďakujem .
Per aspera ad astra
Offline
- (téma jako vyřešené označil(a) vytautas)
#2 16. 08. 2015 22:10
Re: delitele jednotky
v podstate by úloha mala byť ekvivalentná s tvrdením
ak 
ako v prvom príspevku, x neexistuje práve vtedy, keď 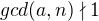 a tak musí byť
a tak musí byť  (ak beriem, že gcd je len kladné)
(ak beriem, že gcd je len kladné)
keď tak teraz rozmýšľam, ako presnejšie dokázať, že ak 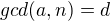 a
a 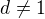 tak potom je
tak potom je  deliteľom nuly, že existuje
deliteľom nuly, že existuje  také,čiže
také,čiže 
ďakujem .
Per aspera ad astra
Offline
#3 17. 08. 2015 14:05 — Editoval vanok (18. 08. 2015 09:11)
Re: delitele jednotky
[img][/img]Ahoj ↑ vytautas:,
Ide o pekne cvicenie, vlasnost ktoru pripomina, je zial akokeby zabudnuta vela studentamy.
Vidim ze si sa snazil preformulovat tvoje cvicenie. Mas tam au dobre myslienky....
Ukazem ti, trochu viac ako to co je formulovane v tvojom cviceni.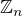 je disjonktna unia mnoziny jeho delitelov jednotky a mnoziny jeho delitelov nuly.
je disjonktna unia mnoziny jeho delitelov jednotky a mnoziny jeho delitelov nuly.
Naviac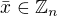 je delitelom jednotky v
je delitelom jednotky v 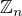 len a len ak
len a len ak 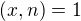
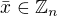 je delitel nuly v
je delitel nuly v 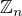 len a len ak
len a len ak 
Nech 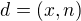 .
.
Ak 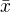 je delitelom jednotky a
je delitelom jednotky a 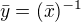 , tak mame
, tak mame  , a preto existuje
, a preto existuje 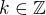 take, ze
take, ze 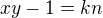 . Co da
. Co da 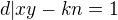 a preto
a preto  .
.
Reciprocne, nech d=1. Bachet-ova veta nam zarucuje, ze existuje 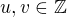 take, ze
take, ze 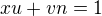 . To nam da
. To nam da  a preto
a preto 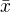 je delitelom jednotky v
je delitelom jednotky v 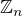 .
.
Edit. Oprava podla beznej pouzivanej sk terminologie
Porozmyslaj o tejto casti dokazu, kde som vyuzil uzitocnu Bachet-ovu vetu.
Zvysok to bude pokracovanie. ( ale nic ti nebrani trochu o tom porozmyslat)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 17. 08. 2015 21:17 — Editoval Brano (17. 08. 2015 21:30)
Re: delitele jednotky
↑ vytautas:
tu mas v podstate "chybu" v dokaze (chybu v zmysle, ze ti tam chyba argumentacia)
totizto vyzera to, ze tvrdis : "a je delitel jednotky" implikuje "(a,n)=1" a teda "a nie je delitel jednotky" implikuje "(a,n)>2" ale takto implikacia nefunguje - v prvom tvrdeni by si potreboval presne opacnu implikaciu
(ktora v skutocnosti plati - pozri Bezoutovu identitu)
Alternativny dokaz:
Nech 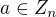 uvazujme vsetky
uvazujme vsetky 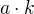 pre
pre 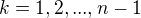 - tento sucin ale moze nadobudat iba hodnoty
- tento sucin ale moze nadobudat iba hodnoty 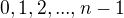 - lebo sme v
- lebo sme v  . Ak je medzi nimi
. Ak je medzi nimi  tak je
tak je  delitelom jednotky; ak nie je, tak bud je medzi nimi nula a sme hotovi, alebo sa tam jedna z moznych hodnot nachadza (aspon) dva krat a teda existuju take
delitelom jednotky; ak nie je, tak bud je medzi nimi nula a sme hotovi, alebo sa tam jedna z moznych hodnot nachadza (aspon) dva krat a teda existuju take  ,
,  , ze plati
, ze plati 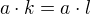 avsak potom
avsak potom 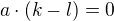 cize
cize  je delitelom nuly.
je delitelom nuly.
Offline
#6 17. 08. 2015 23:30 — Editoval vanok (18. 08. 2015 09:13)
Re: delitele jednotky
Tak ta posledna cast dokazu.
Ak d>1, mame 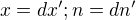 . Potom
. Potom 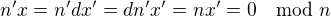 , co znamena, ze
, co znamena, ze 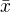 je delitel nuly v
je delitel nuly v 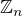 .
.
Reciprocne delitel nuly nemoze byt delitelom jednotky a tak  .
.
Poznamka. Delitel jednotky, je vlastne inverzibiliny ( regularny) prvok (ktore generuju grupu inverzibilnych prvkov, o ktorej sa da dokazat, ze ma 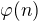 prvkov,
prvkov,  je Euler-ova funkcia).
je Euler-ova funkcia).
Poznamenajme este, ze pojem unité = "jednotka" sa pouziva vo fr., en. namiesto pojmu delitel jednotky.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 18. 08. 2015 01:33
Re: delitele jednotky
↑ vytautas:,
Vies ze 
A chces ukazat, ze 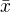 je delitelom nuly.
je delitelom nuly. je dobry kandidat na dokaz prave preto ze
je dobry kandidat na dokaz prave preto ze 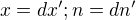 ...
...
Dobre pokracovanie.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#10 18. 08. 2015 22:58 — Editoval vanok (19. 08. 2015 14:47)
Re: delitele jednotky
↑ vytautas:
Doplnok.
Upresnim este co som napisal tu ↑ vanok: v poznamke.
Iste si teraz schopny dokazat toto
Nech 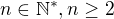 ,
, 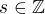 , nasledujuce vlasnosti su ekvivalentne
, nasledujuce vlasnosti su ekvivalentne
1) 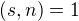
2) 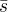 je generator grupy
je generator grupy 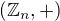
3)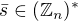 co je grupa intervertibilnych prvkov okruhu
co je grupa intervertibilnych prvkov okruhu 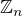
Tento vysledok je dolezity co sa tyka studia automorfizmov groupy 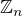 co umozni napr. vysetrenie urcitych semi-direktnych sucinov grup.
co umozni napr. vysetrenie urcitych semi-direktnych sucinov grup.
No vsak to iste prehlbis neskor, ak budes pokracovat vo studiu algebry.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline

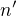 a
a a vedie to k riešeniu ?
a vedie to k riešeniu ?