Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 18. 08. 2015 17:13 — Editoval Akcope (18. 08. 2015 17:19)
Formální definice ordinálního typu
Ahoj, za chvíli mě čekají státnice z programovacích jazyků a přemýšlím jak bych slušně matematicky definoval ordinální typ. Napadlo mě tohle:
Nechť T je typ, jeho kardinalita je n, a 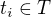
P je konečná podmnožina 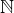
Typ T je ordinální  bijektivní zobrazení
bijektivní zobrazení 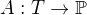 takové, že platí
takové, že platí 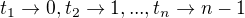
Je to průchozí? Předem díky.
Offline
#2 18. 08. 2015 18:19
- Eratosthenes
- Příspěvky: 2937
- Reputace: 139
Re: Formální definice ordinálního typu
Ahoj, ↑ Akcope:
to by ordinální typ bylo úplně všechno. Všechno, co lze v počítači reprezentovat, totiž má konečný počet hodnot. Jednoduše proto, že každý počítač má konečnou paměť...
Budoucnost patří aluminiu.
Offline
#3 18. 08. 2015 23:27
- check_drummer

- Příspěvky: 5182
- Reputace: 106
Re: Formální definice ordinálního typu
↑ Akcope:
Ahoj, neměl bys na tom typu definovat uspořádání? Sice to bude asi to indukované tou bijekcí A, ale asi by definováno být mělo....
"Máte úhel beta." "No to nemám."
Offline
#4 19. 08. 2015 17:34
- Eratosthenes
- Příspěvky: 2937
- Reputace: 139
Re: Formální definice ordinálního typu
ahoj ↑ check_drummer:,
uspořádání nestačí - uspořádána jsou i reálná čísla ...
Budoucnost patří aluminiu.
Offline
#5 19. 08. 2015 22:28
- check_drummer

- Příspěvky: 5182
- Reputace: 106
Re: Formální definice ordinálního typu
↑ Eratosthenes:
Ahoj, já sice neříkám, že to stačí - ale na druhou stranu to tak asi je - pokud definujeme na dané struktuře dobré uspořádání, tak máme ordinální typ. (I reálná čísla lze s axiomem výběru dobře uspořádat.)
"Máte úhel beta." "No to nemám."
Offline
#6 19. 08. 2015 23:54
- Eratosthenes
- Příspěvky: 2937
- Reputace: 139
Re: Formální definice ordinálního typu
↑ check_drummer:
ahoj - že uspořádání má být dobré, to jsi řekl až teď :-) Nicméně se obávám, že ani to nestačí. Reálná čísla a reálný typ je bohužel něco jiného. Už proto, že prvků reálného typu je (na rozdíl od reálných čísel) pouze konečný počet, takže na jeho uspořádání (ani to dobré) axiom výběru nepotřebuješ.
Pomohl bych siaxiomy přirozených čísel: Typ je ordinální právě tehdy, když jsou na něm definovány funkce následovník (stejně jako v N s tím, že existuje právě jeden, který následovníka nemá) a předchůdce - existuje právě jeden který ho nemá...
Budoucnost patří aluminiu.
Offline
#7 20. 08. 2015 23:44
- check_drummer

- Příspěvky: 5182
- Reputace: 106
Re: Formální definice ordinálního typu
↑ Eratosthenes:
Tak jestli je to ordinální typ uvažovaný v informatice (=konečný), pak to není moc zajímavé...
"Máte úhel beta." "No to nemám."
Offline
#8 21. 08. 2015 16:30
- Eratosthenes
- Příspěvky: 2937
- Reputace: 139
Re: Formální definice ordinálního typu
↑ check_drummer:
Na státnice z programovacích jazyků bych to tak nějak viděl. Pokud by to mělo být v širších souvislostech, pak bych to viděl spíš na definici ordinálních čísel, ale ta je taky dost známá...
Budoucnost patří aluminiu.
Offline
#9 22. 08. 2015 17:08
- check_drummer

- Příspěvky: 5182
- Reputace: 106
Re: Formální definice ordinálního typu
↑ Eratosthenes:
Zajímavé by bylo sestrojit vhodnou reprentaci konečné podmnožiny ordinálních čísel. To by asi smysl dávalo, ale tam bych zase řekl, že by asi nebylo možné tuto reprezentaci sestrojit - pokud by byla dvě čísla vzdálena od sebe o nekonečný počet ordinálních čísel.
"Máte úhel beta." "No to nemám."
Offline
