Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 03. 09. 2015 11:59
- terezkaaaaa5

- Příspěvky: 1221
- Reputace: 2
Integrál
Dobrý den, mám příklad:  . Jakou prosím použít substituci?
. Jakou prosím použít substituci?
Offline
- (téma jako vyřešené označil(a) terezkaaaaa5)
#2 03. 09. 2015 12:08
#3 03. 09. 2015 12:14
- terezkaaaaa5

- Příspěvky: 1221
- Reputace: 2
Re: Integrál
↑ Cheop:
Díky. Ale když v zadání žádný cos x není? Tak mám použít vzorec  ? A integrál napíši jako:
? A integrál napíši jako: 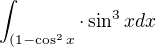 ?
?
Offline
#4 03. 09. 2015 12:31
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Integrál
↑ terezkaaaaa5:
Goniometrickou jedničku použiješ až po substituci.
Měla bys dospět k integrálu
-int(1-cos^2 x)^2
Nikdo není dokonalý
Offline
#5 03. 09. 2015 12:37
- terezkaaaaa5

- Příspěvky: 1221
- Reputace: 2
Re: Integrál
↑ Cheop:
Bohužel vůbec netuším jak. Jak v zadání, kde žádný cosinus nemám, mám substituovat cos? Když vzoreček mám použít až po substituci?
Offline
#6 03. 09. 2015 12:52 — Editoval Cheop (03. 09. 2015 12:54)
#8 03. 09. 2015 15:15
Re: Integrál
↑ terezkaaaaa5:
Dobrý den.
Derivace výsledku dá Odkaz, takže bych řekl, že je někde problém se znaménkem - asi tady: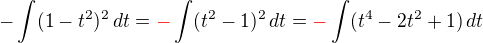
Pokud se tedy nemýlím.
Online
#9 03. 09. 2015 15:19
- terezkaaaaa5

- Příspěvky: 1221
- Reputace: 2
Re: Integrál
Díky. co ale nechápu je, jak se z  stane
stane ? Moc děkuji za objasnění.
? Moc děkuji za objasnění.
Offline
#10 03. 09. 2015 15:33
Re: Integrál
↑ terezkaaaaa5:
Protože vytknutím (-1) ze 'závorky na druhou' se znaménko nezmění:
Pokud se tedy nemýlím.
Online
#12 04. 09. 2015 10:39
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Integrál
Zdravím,
↑ Cheop: pořád ale s touto formou zápisu (2 proměnné v jednom integrálu) nemohu souhlasit a hlavně takový přístup zamlžuje princip substituční metody - že v zápisu vidím složenou funkci a derivaci vnitřní funkce.
terezkaaaaa5 napsal(a):
A integrál napíši jako:
to nebyla nejhorší idea, jen více dotáhnout "A integrál napíši jako": teď substituce kolegy Cheopa. A tak se musím snažit provádět úpravy, abych viděla funkci a derivaci vnitřní.
teď substituce kolegy Cheopa. A tak se musím snažit provádět úpravy, abych viděla funkci a derivaci vnitřní.
↑ Cheop: :-) podstatné je, pravda, že konečně déšť zamlžuje okna. Zdravím, také bratra.
Offline




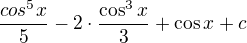 ?
?