Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 27. 09. 2015 22:12 — Editoval jelena (30. 09. 2015 13:09)
Dôkaz indukciou
Ahojte, vedeli by ste mi prosím vysvetliť ako matematickou indukciou dokážem toto? Vďaka :)
Jelena: edit: jak ukázala následná diskuse, uvedený vztah nebyl platný (a v příspěvku č. 8 kolega vanok navrhl možné znění úlohy, které je dále diskutováno)
Offline
#2 27. 09. 2015 23:24
#3 27. 09. 2015 23:42
Re: Dôkaz indukciou
↑ Eratosthenes: hop,prave pozeram,ze som zabudla uviest podmienky,  su kladne :)
su kladne :)
Offline
#8 28. 09. 2015 15:49 — Editoval vanok (28. 09. 2015 15:49)
Re: Dôkaz indukciou
Pozdravujem
Nechcela si dokazat ze
Pre ostro kladne realne 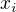 ?
?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 28. 09. 2015 16:38
Re: Dôkaz indukciou
ahoj, našla som v inej knihe aj prvé dve časti tohto príkladu (bez ktorých to nejde) a postupovala som takto:
1. Dokážte, že platí: ak a
a  , potom
, potom  .
.
Dôkaz: 
 a to platí aj pre
a to platí aj pre 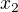 = 0 (
= 0 ( ) aj pre x_{2} iné od 0 (
) aj pre x_{2} iné od 0 ( )
)
2. Na základe toho dokážte, nech  sú kladné čísla také, že
sú kladné čísla také, že  potom
potom .
.
Dôkaz:
-čiže ak platí, že  , potom
, potom  a
a  (čo je vlastne to isté ako v prvom príklade, čiže
(čo je vlastne to isté ako v prvom príklade, čiže  )
)
-ak použijeme predpoklad, že to bude platiť aj pre k+1, potom to vyzerá takto (z 1. príkladu)
 (čo platí)
(čo platí)
a teraz sa dostávame k prípadu číslo 3 (ktorý mi robí problém), kedy
a) 
b)![kopírovat do textarea $\sqrt[n]{x_{1}x_{2}...x_{n}}\le \frac{1}{n}$](/mathtex/8b/8bea9958d562aa584be465738fb67a41.gif)
kde  sú kladné čísla
sú kladné čísla
Offline
#10 28. 09. 2015 17:31
Re: Dôkaz indukciou
Ahoj
Mas tam naznak dokazu vdaka GA nerovnosti.
No vsak to sa da pouzit len v pripade ktory popisujem ↑ vanok:
Vtedy dostanes ![kopírovat do textarea $\frac{x_{1}}{x_{2}}+\frac{x_{2}}{x_{3}}+...+\frac{x_{n-1}}{x_{n}}+\frac{x_n}{x_1}\ge n\sqrt[n]{\frac{x_{1}}{x_{2}}*\frac{x_{2}}{x_{3}}*...*\frac{x_{n-1}}{x_{n}}*\frac{x_n}{x_1}}=n$](/mathtex/2a/2a077e3212cce2b9bca193994e3cc981.gif)
(Ako vidis pod odmocninou mam 1, a ty nie).
To ukoncuje dokaz.
Ale skutocne viem to dokazat aj indukciou.
Mozem ti v tom pomoct. Ale najprv si uvedom chyby v tvojom zadani. ( ak je to skutocne tak ako pises v nejakek knihe, tak ju hod okamzite do kosa !)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#11 30. 09. 2015 00:08
Re: Dôkaz indukciou
Ako vidim nic nove, co sa tyka dokazu.
Mimoriadne tu dam navod na riesenie indukciou, problemu vo forme ako treba ↑ vanok: ako som to napisal vysie.
Robim to len preto, lebo ide o trochu delicatny dokaz.
Nerovnost  pre
pre  ,
,
Plati pre n=2,.......
Kontrola
Pokracujme z dokazom.
Predpokladajme, ze vzorec plati pre n-1 lubovolnych cisiel >0.
Tak pre n ostro pozitivnych cisiel
 aplikujme
aplikujme vzorec na
 prvych z nich, co da
prvych z nich, co da  .
.Aby sme dokazali, ze

staci aby
 ,
, 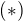
Teraz treba mat dobru trochu trikovu myslienku. Aby som ti celkom nepokazil radost, po hladani pozri na to co tu je skryte.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#13 30. 09. 2015 09:40
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Dôkaz indukciou
Zdravím,
dle zprávy kolegy vanok v reportech moderátorům přesouvám do zajímavých, jen bych chtěla doplnit do úvodního příspěvku ještě správné zadání (původní příspěvek ponechám celý), jen co, prosím, mám doplnit? Děkuji.
Offline
#14 30. 09. 2015 11:15
Re: Dôkaz indukciou
Pozdravujem ↑ jelena:
Moj prispevk #8 obsahuje spravnu formu textu cvicenia.
Skutocne v povodnom prispevku chyba jeden scitanec. Preto ako ukazali prve prispevky nemohol mat ani riesenie.
No ale pre citatela moze ist o poucnu chybu.
Ako sa da vidiet v #10 existuje aj jednoriadkove riesenie vdaka GA nerovnosti (GA=geometricko-arimetmeticka).
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#15 30. 09. 2015 13:11
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Dôkaz indukciou
↑ vanok: zdravím a děkuji za upřesněni, přidala jsem odkaz do ↑ úvodního příspěvku:.
Offline

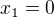 ,
, 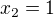 . Pak je
. Pak je 


 je najmensie z nich, vtedy
je najmensie z nich, vtedy 