Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 02. 10. 2015 10:30
- miso16211
- Πυθαγόραc
- Příspěvky: 1522
- Pozice: n/a
Vzorec. vzťah nevíem k čomu
Zdravím, k čomu sa môže viazať tento vzťah je to nejaká stredna hodnota intenzity, ale vôbec neviem, či je správny vzťah a je len nesprávne pripradenie, alebo je nesprávny vzťah.
Offline
#2 02. 10. 2015 14:01
Re: Vzorec. vzťah nevíem k čomu
↑ miso16211:
Ahoj,
skutešně to vypadá na intenzitu veličiny f "od teď navěky". Nějaký smysl to mít může, ale užitečnější by mi přišlo hnát limitou T k nule, pak by to byla intenzita veličiny f v čase t.
Доктор сказал «в морг» — значит в морг!
Offline
#3 03. 10. 2015 18:55 — Editoval miso16211 (03. 10. 2015 19:25)
- miso16211
- Πυθαγόραc
- Příspěvky: 1522
- Pozice: n/a
Re: Vzorec. vzťah nevíem k čomu
↑ Formol: vobec tomu nerozumiem, ta funkcia f, je zavisla na nejakej premennej tau (tau je čas, obecne značený " t "?). Proste neviem čo tam robi  a
a 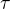 .
.
Inak stredná intenzita veličiny je 
este je moznost takáto: 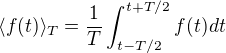
no a ak chceme zistit strednu hodnotu nejakej veliciny na nekonecnom malom intevale snad by tam mohla ist limita, ale preco tá funkcia je na druhú, a preco je integrovaná podla neznámen premennej, to neviem.
Offline
#4 04. 10. 2015 11:14
Re: Vzorec. vzťah nevíem k čomu
↑ miso16211: Ahoj, pozri prípadne aj funkciu RMS
https://en.wikipedia.org/wiki/Root_mean_square
Offline
#5 04. 10. 2015 11:22
Re: Vzorec. vzťah nevíem k čomu
↑ miso16211:
Tak ono takhle bez kontextu to nebude vědět niko. Asi by bylo nejlepší říct, kde si k tomu vzorci přišel
1. Proč je integrovaná podle neznámé proměnné?-Tam jde jen o to, že zápis například 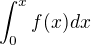 není moc pěkný. Tak aby se ti nemíchal čas v mezích a navíc k otmu v intergrandu, tak se prostě proměná označí jinak.
není moc pěkný. Tak aby se ti nemíchal čas v mezích a navíc k otmu v intergrandu, tak se prostě proměná označí jinak.
2. Střední hodnota na nekonečně malém intervalu je rovna funkční hodnotě
3. Ten vzorec ti prakticky říká střední hodnotu ve "velkém" časovém úseku. (ideálně nekonečném)
Offline
#6 04. 10. 2015 11:42
- miso16211
- Πυθαγόραc
- Příspěvky: 1522
- Pozice: n/a
Re: Vzorec. vzťah nevíem k čomu
↑ Brzls:
ten vzťah nám napísal vyučujúci (ktorý je čech, a možno v česku sa to tak preberá na optike),a mam napsiane že je to stredná hodnota intenzity a že s tym študenti maju problém.
Ja mam problém s tým že tá funkcia je na druhú.
Offline
