Matematické Fórum

xstudentíkx · 05. 10. 2015 17:53

Ahoj,

nedaří se mi dokázat toto tvrzení, jenž se týká nekonečných řad.

Budiž z libovolné, ale ne celé záporné, budiž k přirozené číslo. Položme: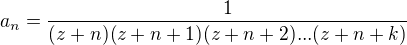

$a_{n}=\frac{1}{(z+n)(z+n+1)(z+n+2)...(z+n+k)}$

Potom je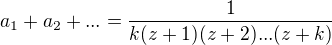

$a_{1}+a_{2}+...=\frac{1}{k(z+1)(z+2)...(z+k)}$

Dále je přidána tato ekvivalence u které je mi zřejmé, že platí.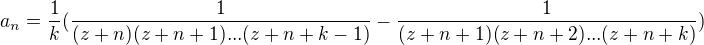

$a_{n}=\frac{1}{k}(\frac{1}{(z+n)(z+n+1)...(z+n+k-1)}-\frac{1}{(z+n+1)(z+n+2)...(z+n+k)})$

Potřebuji trochu poradit se začátkem. Pár věcí jsem už zkoušela, ale točím se pouze v kruhu a k ničemu novému to nevede.

jarrro · 05. 10. 2015 18:04 — Editoval jarrro (05. 10. 2015 18:08)

keď použiješ dlhšiu definíciu a_n tak v súčte sa ti skoro všetko odčíta
$\tiny{}a_{1}+a_{2}+...=\frac{1}{k}$\frac{1}{(z+1)(z+2)...(z+k)}-\frac{1}{(z+2)(z+3)...(z+k+1)}+\frac{1}{(z+2)(z+3)...(z+k+1)}-\frac{1}{(z+3)(z+4)...(z+k+2)}+\cdots$=\nl =\frac{1}{k(z+1)(z+2)...(z+k)}$

xstudentíkx · 05. 10. 2015 19:26

↑ jarrro:

Děkuji za utvrzení mého postupu. Problém je v tom, že jsem odčítala pomocí převodu na spol. jmenovatele a pořád se, tak točila v tom samém....

Matematické Fórum

#1 05. 10. 2015 17:53

nekonečné řady-důkaz

#2 05. 10. 2015 18:04 — Editoval jarrro (05. 10. 2015 18:08)

Re: nekonečné řady-důkaz

#3 05. 10. 2015 19:26

Re: nekonečné řady-důkaz

Zápatí